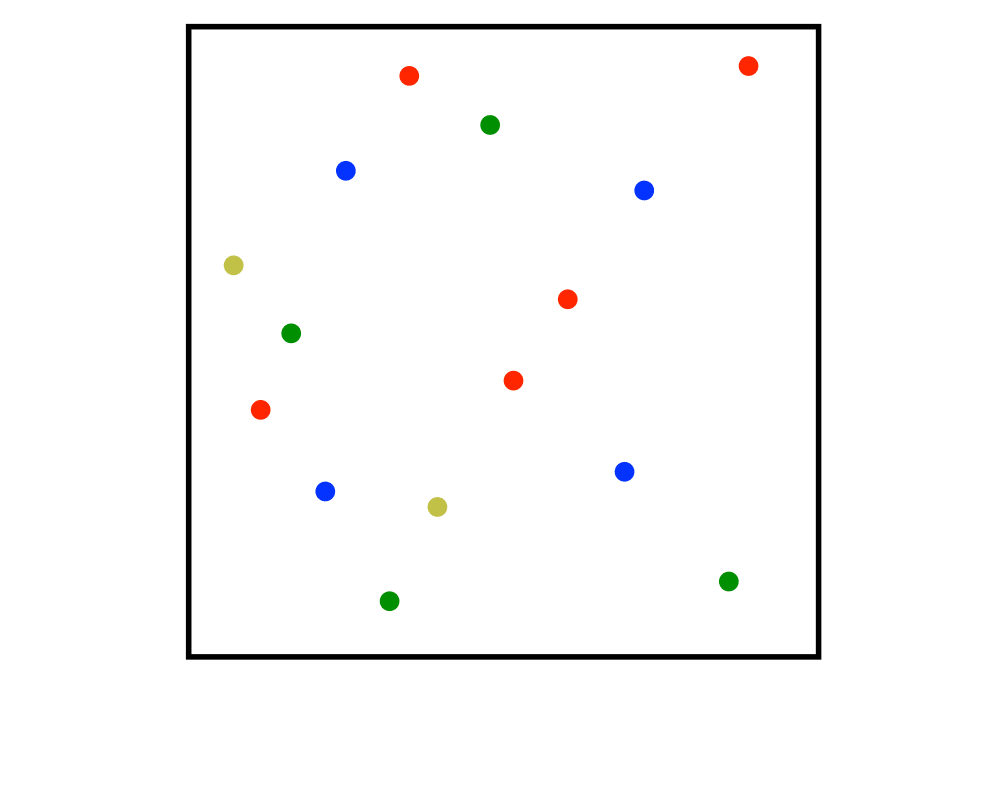
 |
 |
|
|
Input Description: A set \(S\) of \(n\) points in \(k\)-dimensions.
Problem: Construct a tree which partitions the space by half-planes such that each point is contained in it is own region.
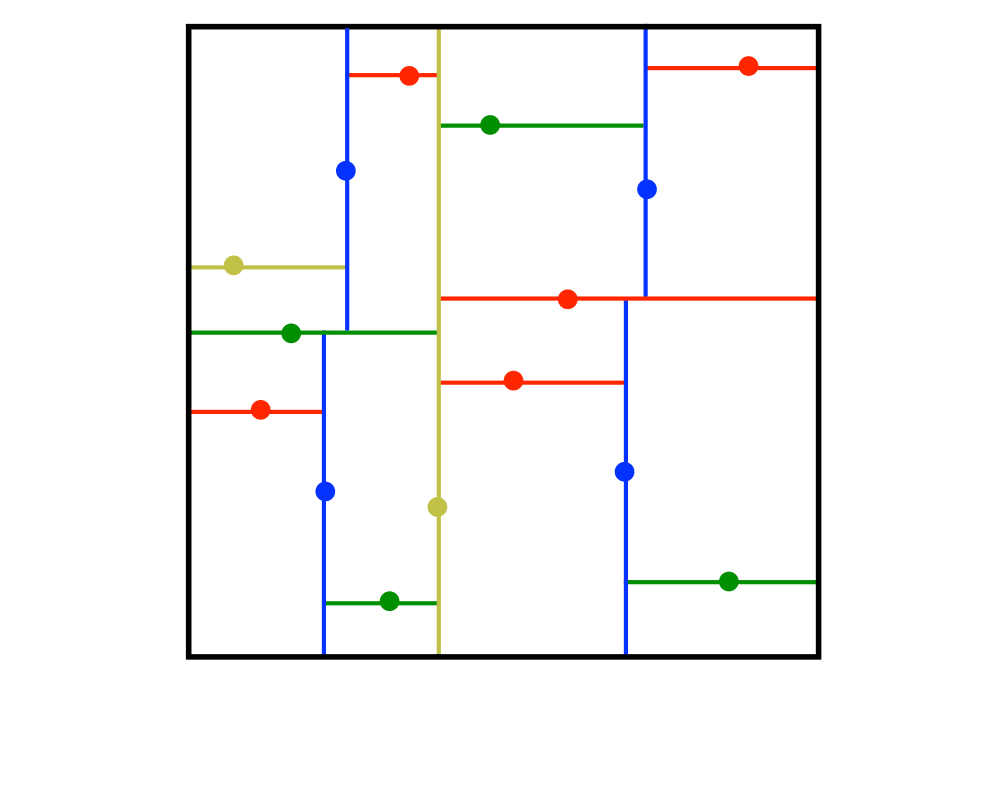
Excerpt from The Algorithm Design Manual: Although many different flavors of kd-trees have been devised, their purpose is always to hierarchically decompose space into a relatively small number of cells such that no cell contains too many input objects. This provides a fast way to access any input object by position. We traverse down the hierarchy until we find the cell containing the object and then scan through the few objects in the cell to identify the right one.
Typical algorithms construct kd-trees by partitioning point sets. Each node in the tree is defined by a plane through one of the dimensions that partitions the set of points into left/right (or up/down) sets, each with half the points of the parent node. These children are again partitioned into equal halves, using planes through a different dimension. Partitioning stops after lg n levels, with each point in its own leaf cell. Alternate kd-tree construction algorithms insert points incrementally and divide the appropriate cell, although such trees can become seriously unbalanced.
| KDTREE (rating 10) |
Samest Spatial Index Demos (rating 9) |
| Terralib (rating 9) |
nanoflann (rating 8) |
| libkdtree++ (rating 8) |
kdtree (rating 7) |
| java-algorithm-implementation (rating 7) |
DIMACS (rating 0) |
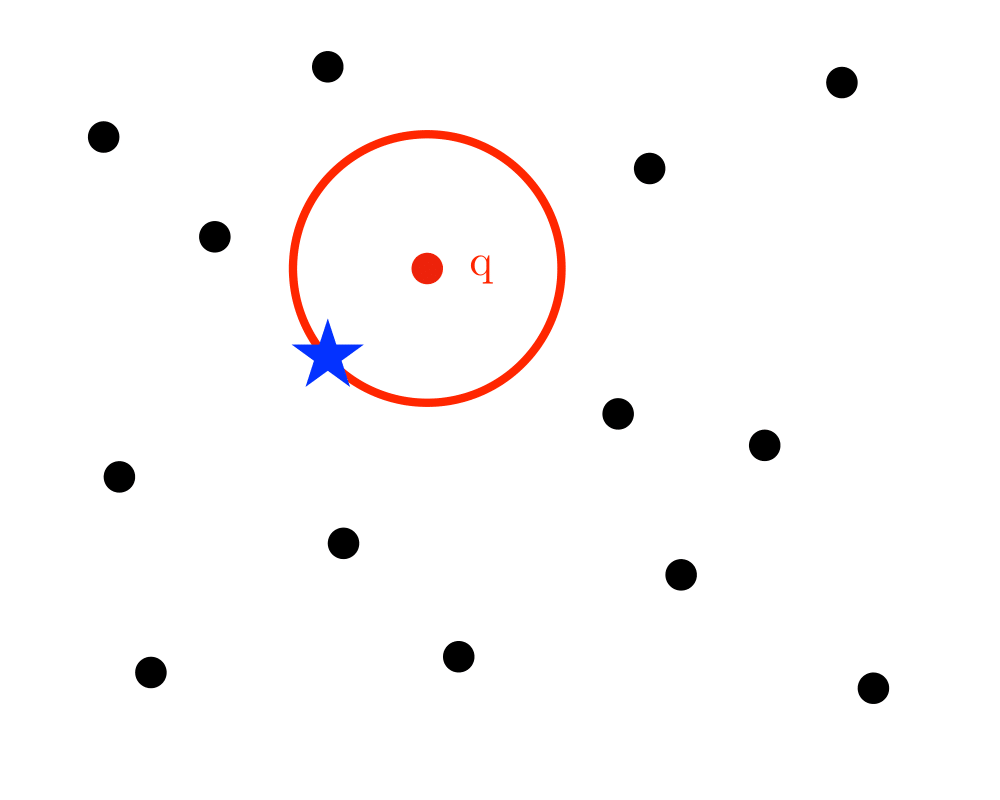  Nearest Neighbor Search |
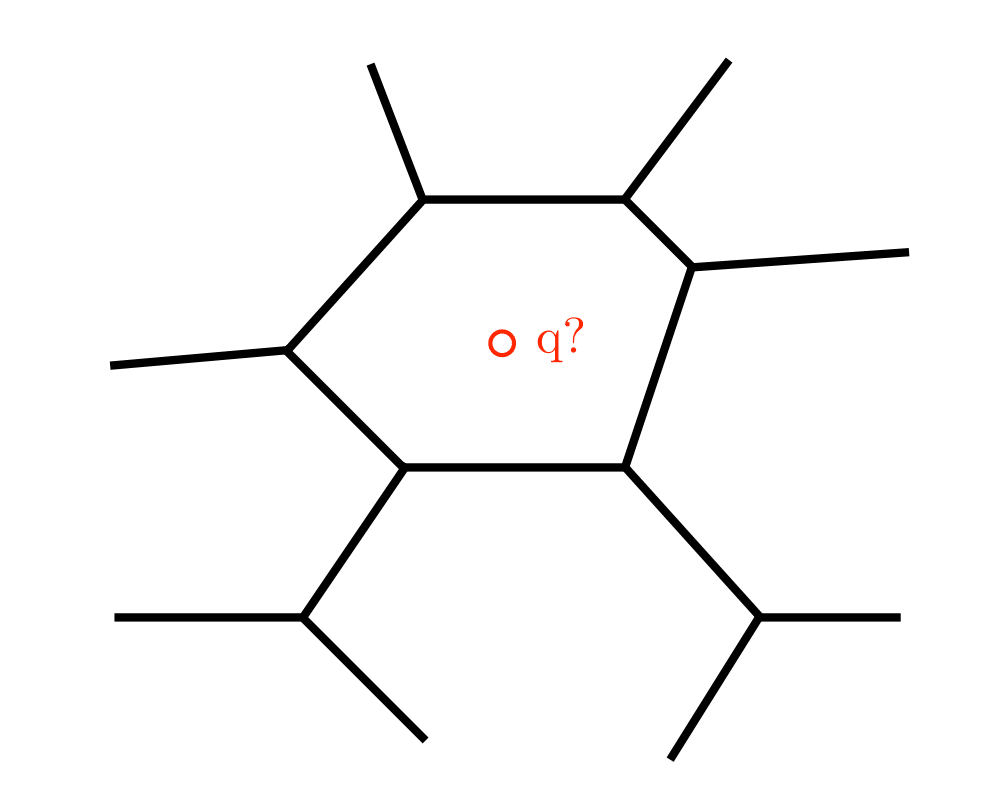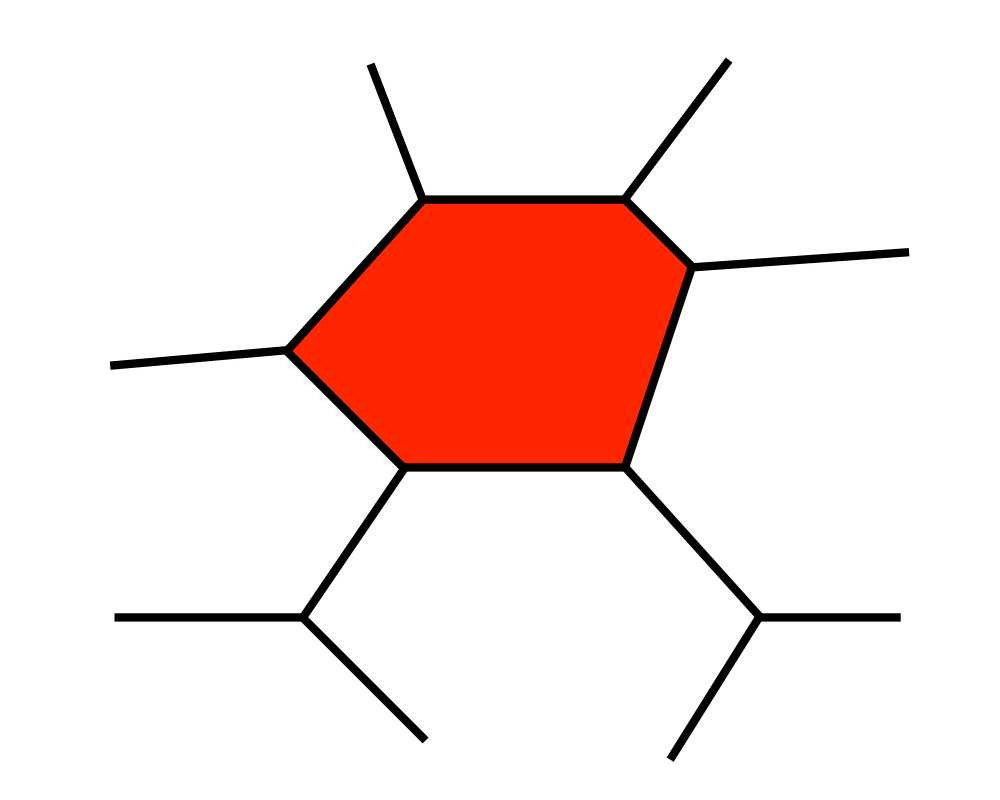  Point Location |
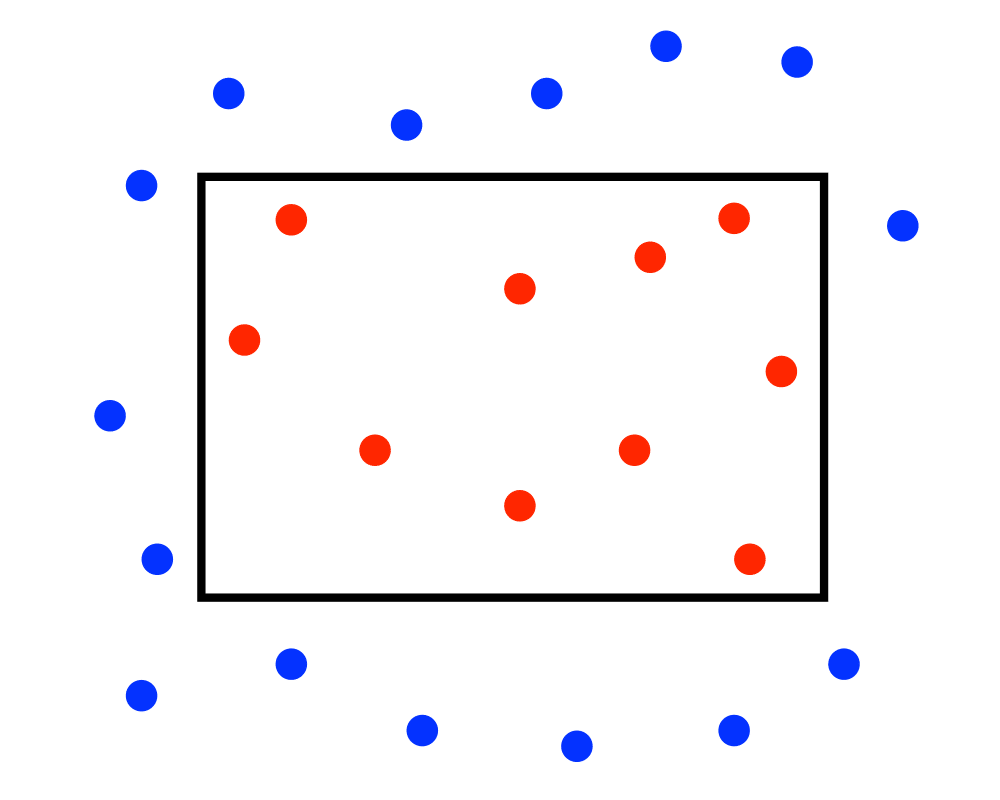  Range Search |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
.jpg)
Data Structures and Algorithm Analysis in C++ (3rd Edition) by Mark Allen Weiss
Foundations of Multidimensional and Metric Data Structures by H. Samet
Data Structures, Near Neighbor Searches, and Methodology: Fifth and Sixth Dimacs Implementation Challenges by Michael H. Goldwasser and Catherine C. McGeoch