Input

Output

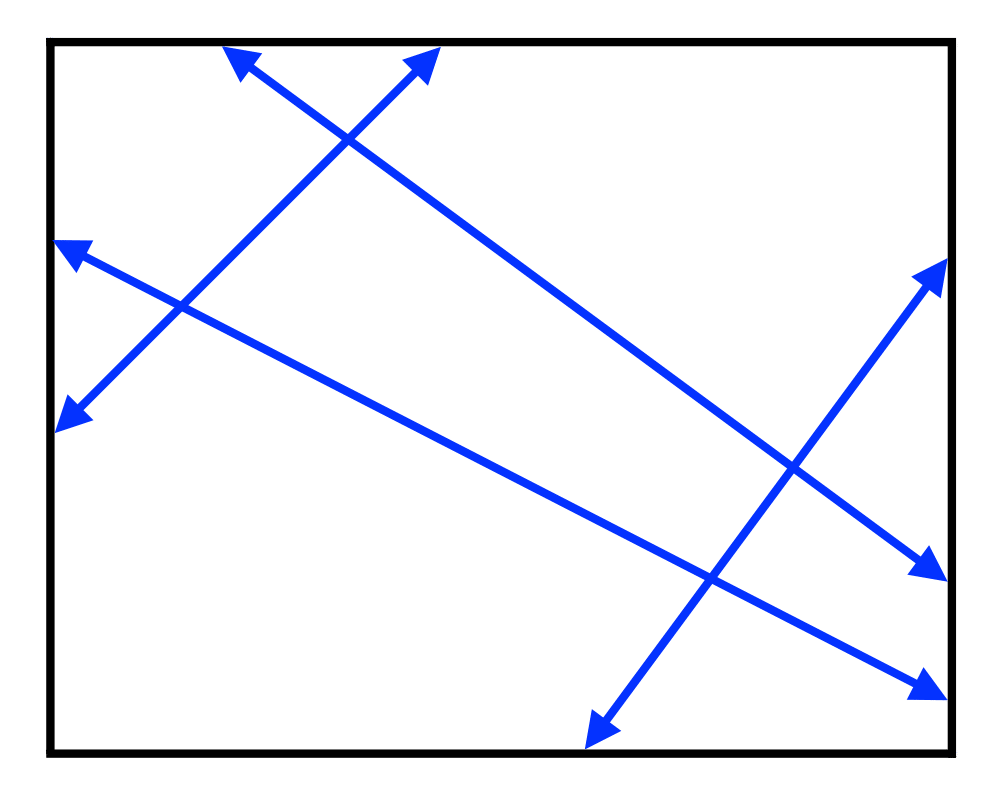
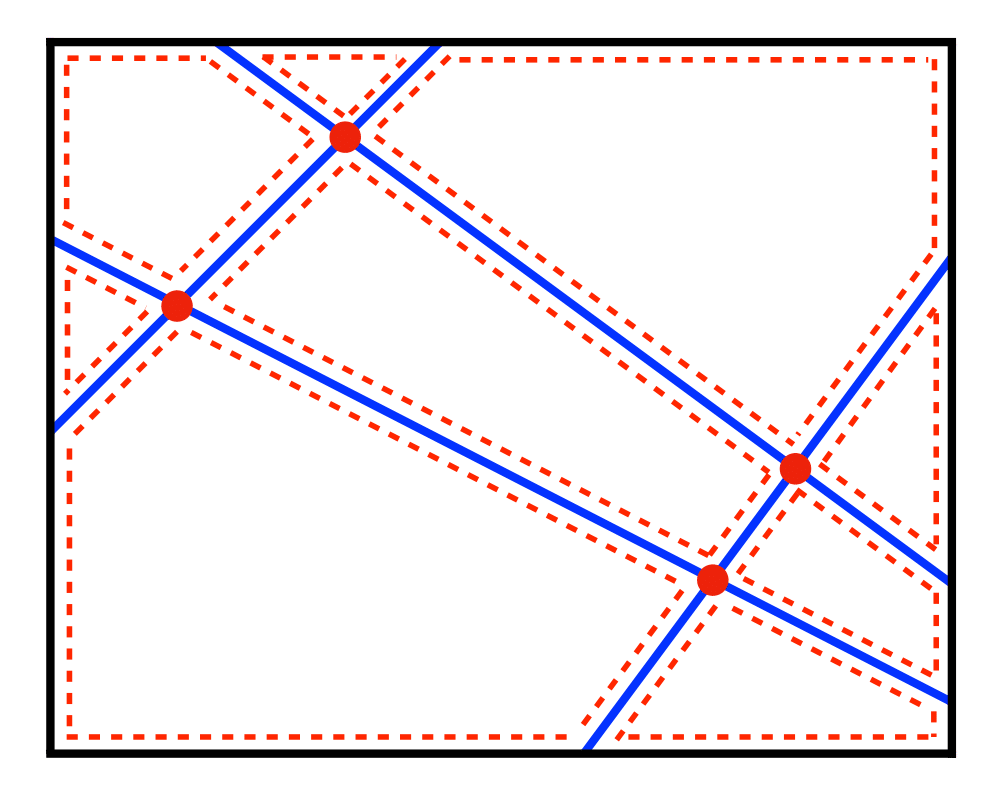
Input Description: A set of lines and line segments \(l_1,...,\l_n\).
Problem: What is the decomposition of the plane defined by \(l_1,...,\l_n\)?

Excerpt from The Algorithm Design Manual: One of the most fundamental problems in computational geometry is constructing arrangements of lines, that is, explicitly building the regions formed by the intersections of a set of \(n\) lines. Algorithms for a surprising number of problems are based on constructing and analyzing the arrangement of a specific set of lines:

• Degeneracy testing -- Given a set of \(n\) lines in the plane, do any three of them pass through the same point? Brute-force testing of all triples takes \(O(n³)\) time. Instead, we can construct the arrangement of the lines and then walk over each vertex and explicitly count its degree, all in quadratic time.

• Satisfying the maximum number of linear constraints -- Suppose that we are given a set of \(n\) linear constraints, each of the form \(y less and or equal to a_i x + b_i\). Which point in the plane satisfies the largest number of them? Construct the arrangement of the lines. All points in any region or cell of this arrangement satisfy exactly the same set of constraints, so we need to test only one point per cell in order to find the global maximum.

Implementations

cgal (rating 10)	Topological Sweep in Degenerate Cases (rating 9)
CGAL (rating 8)	Arrange (rating 7)
LEDA (rating 4)

Recommended Books

Davenport-Schinzel sequences and their geometric applications by M. Sharir and P. Agarwal

Computational Geometry in C by Joseph O'Rourke

Algorithms in Combinatorial Geometry by Herbert Edelsbrunner

Related Problems

Robust Geometric Primitives

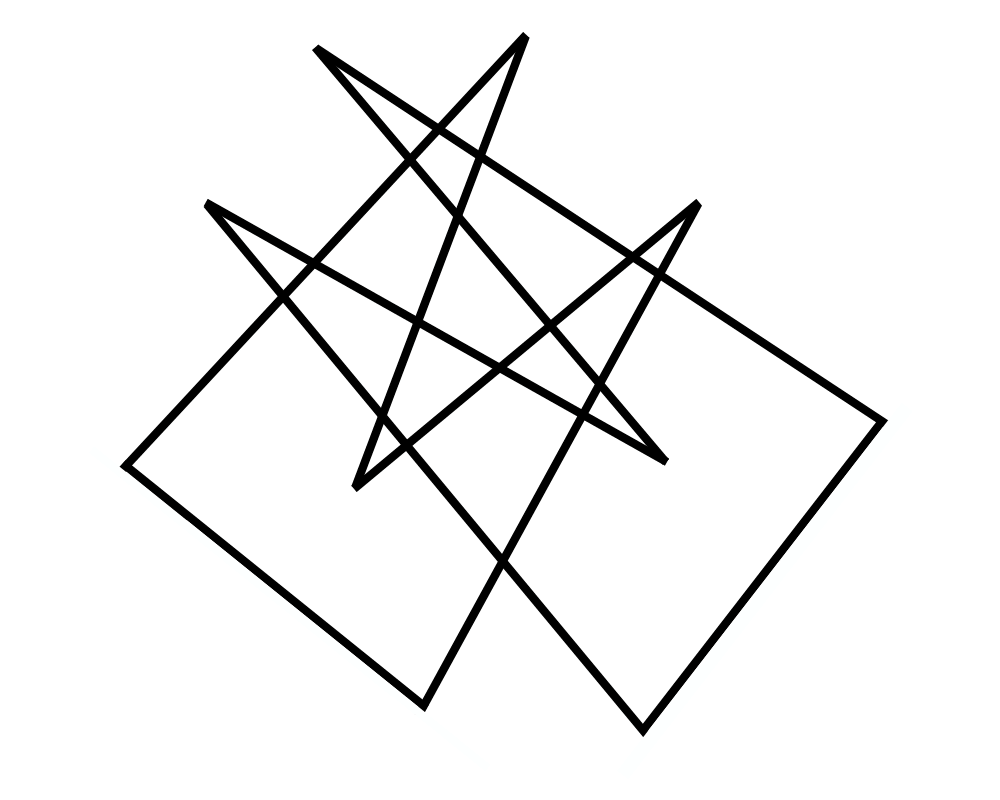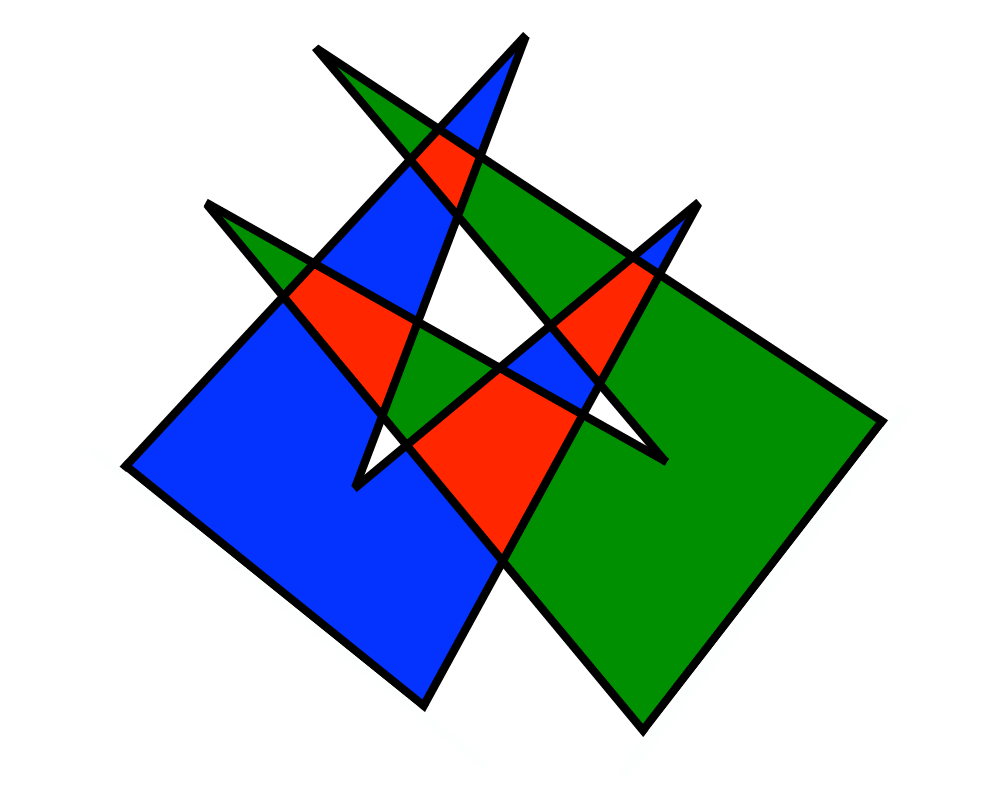Intersection Detection

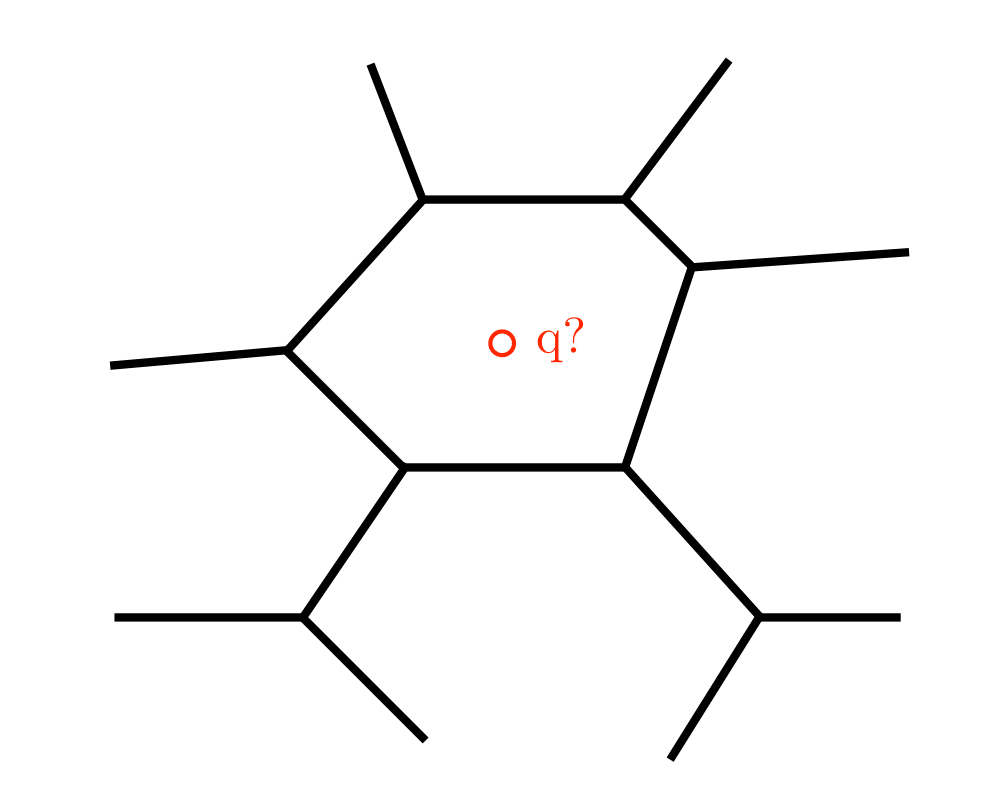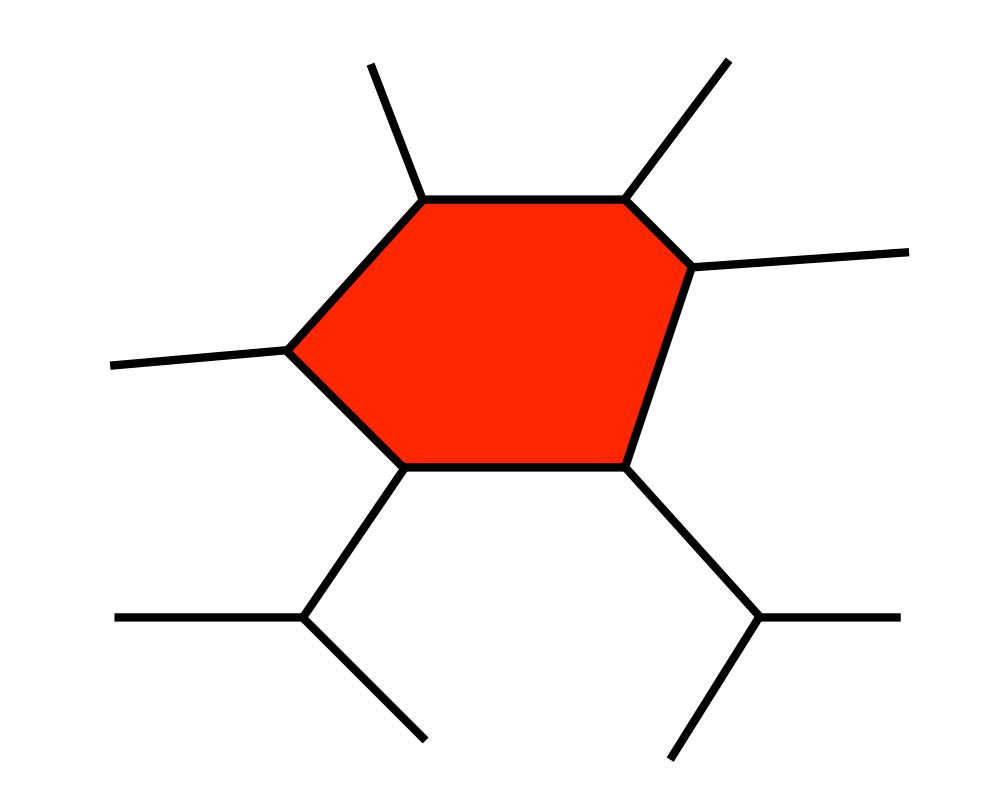Point Location

As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.