 |
 |
|
|
Input Description: Point sets or polygons \(A\) and \(B\), with \(n\) and \(m\) vertices, respectively.
Problem: What is the convolution of \(A\) and \(B\), ie. the Minkowski sum \(A+B = \{x+y| x\in A, y \in B\}\)?
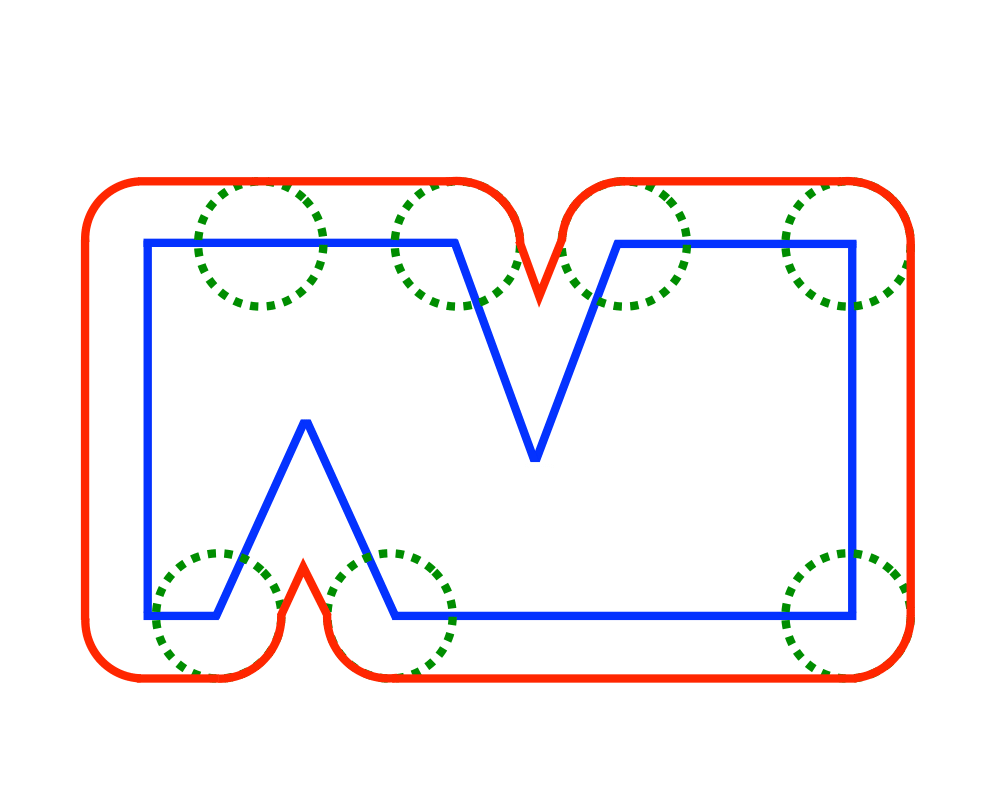
Excerpt from The Algorithm Design Manual: Minkowski sums are useful geometric operations that can be used to fatten objects in appropriate ways. For example, a popular approach to motion planning for polygonal robots in a room with polygonal obstacles fattens each of the obstacles by taking the Minkowski sum of them with the shape of the robot. This reduces the problem to moving a point from the start to the goal using a standard shortest-path algorithm. Another application is in shape simplification where we fatten the boundary of an object to create a channel and then define as the shape the minimum link path lying within this channel. Similarly, convolving an irregular object with a small circle will help smooth out the boundaries by eliminating minor nicks and cuts.
| cgal (rating 10) |
CGAL (rating 10) |
| Efi Fogel's Minkowski Sums and Collision Detection Software (rating 8) |
convex-minkowski-sum (rating 5) |
| BIPM (rating 4) |
 Computational Geometry : Algorithms and Applications by Mark De Berg, Marc Van Kreveld, Mark Overmars, and O. Schwartskopf |
 Computational Geometry in C by Joseph O'Rourke |
  Motion Planning |
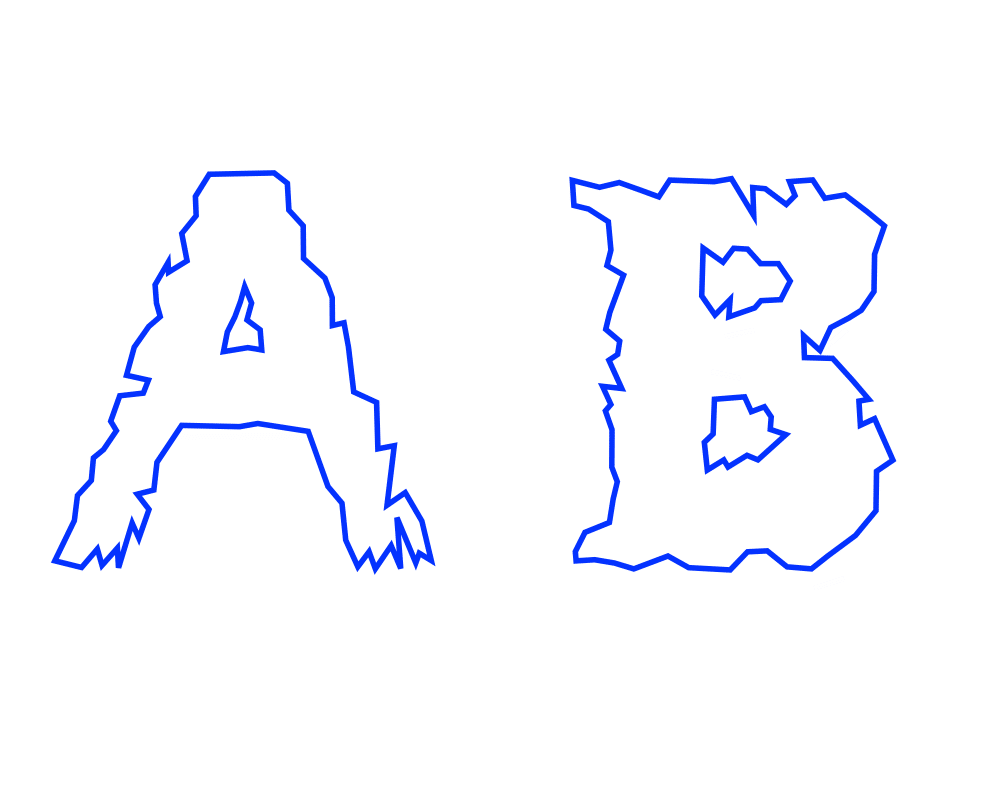  Simplifying Polygons |
  Medial-Axis Transform |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.