 |
 |
|
|
Input Description: A directed graph \(G=(V,E)\).
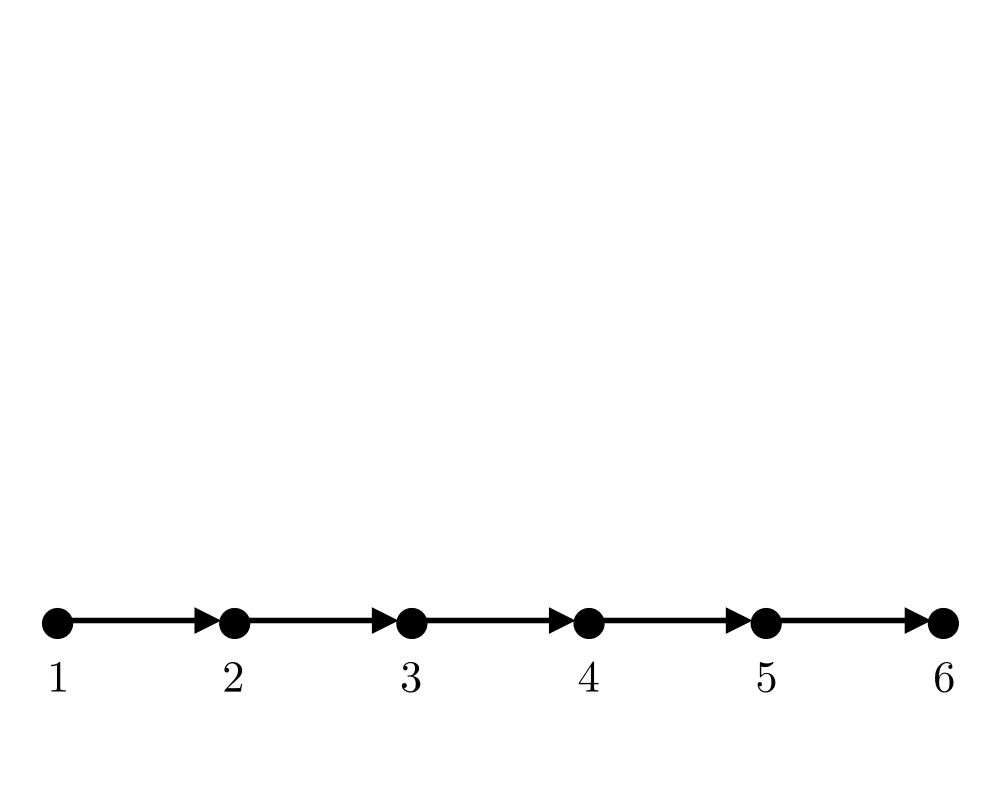
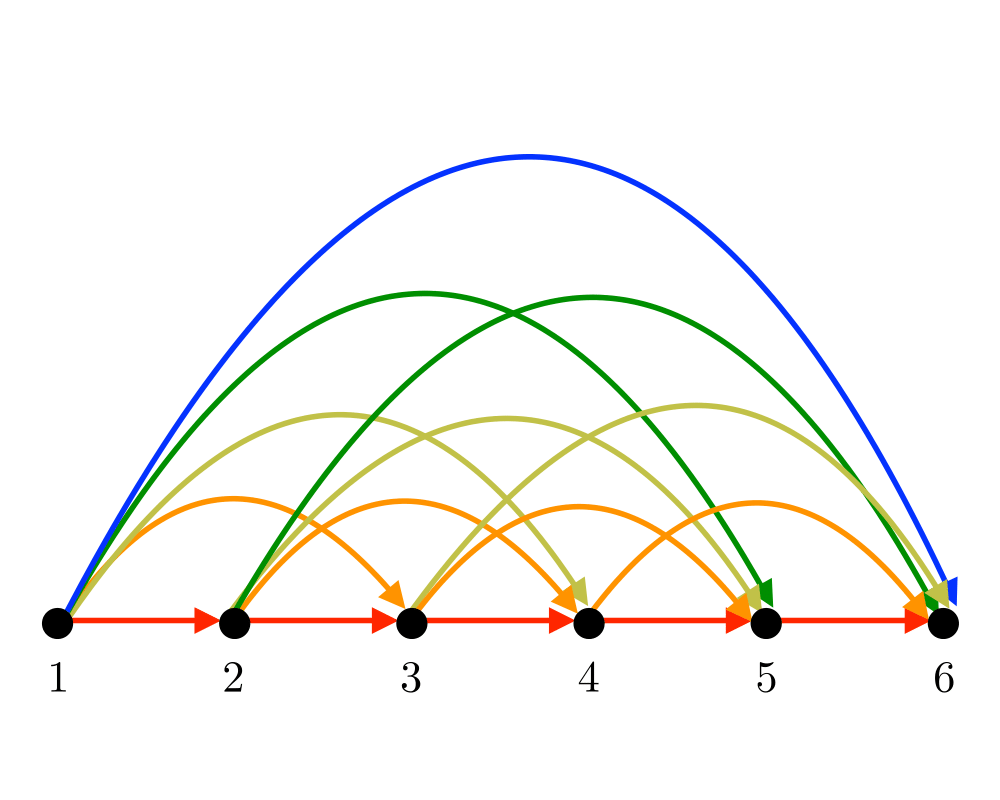
Problem: For transitive closure, construct a graph \(G'=(V,E')\) with edge \((i,j) \in E'\) iff there is a directed path from \(i\) to \(j\) in \(G\). For transitive reduction, construct a small graph \(G'=(V,E')\) with a directed path from \(i\) to \(j\) in \(G'\) iff \((i,j) \in E\).
Excerpt from The Algorithm Design Manual: Transitive closure can be thought of as establishing a data structure that makes it possible to solve reachability questions (can I get to \(x\) from \(y\)?) efficiently. After the preprocessing of constructing the transitive closure, all reachability queries can be answered in constant time by simply reporting a matrix entry. Transitive closure is fundamental in propagating the consequences of modified attributes of a graph \(G\). For example, consider the graph underlying any spreadsheet model, where the vertices are cells and there is an edge from cell \(i\) to cell \(j\) if the result of cell \(j\) depends on cell \(i\). When the value of a given cell is modified, the values of all reachable cells must also be updated. The identity of these cells is revealed by the transitive closure of \(G\). Many database problems reduce to computing transitive closures, for analogous reasons.
| Boost Graph Library (rating 10) |
C++ Boost Library (rating 10) |
| java-algorithms-implementation (rating 7) |
algorithms.js (rating 7) |
| graphlib (rating 7) |
LEDA (rating 5) |
| Combinatorica (rating 4) |
  Connected Components |
  Shortest Path |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica by S. Pemmaraju and S. Skiena
Handbook of Theoretical Computer Science : Algorithms and Complexity by J. Van Leeuwen
The Design and Analysis of Computer Algorithms by A. Aho and J. Hopcroft and J. Ullman