 |
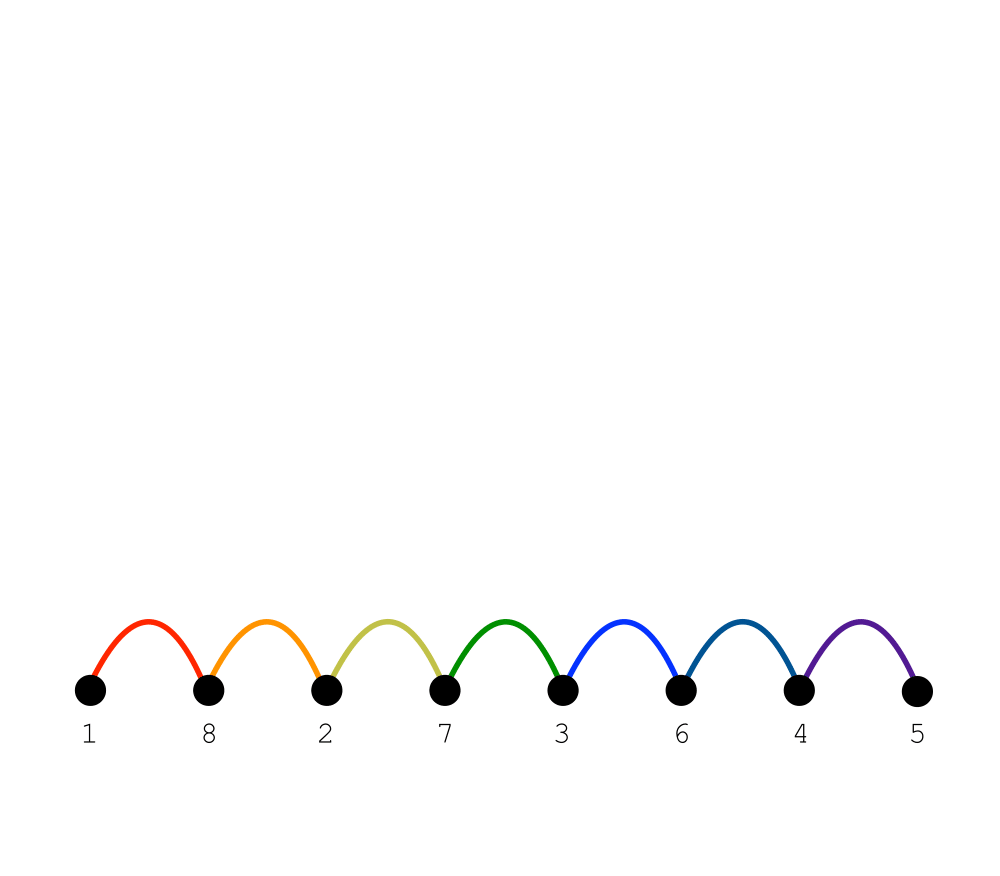 |
 |
 |
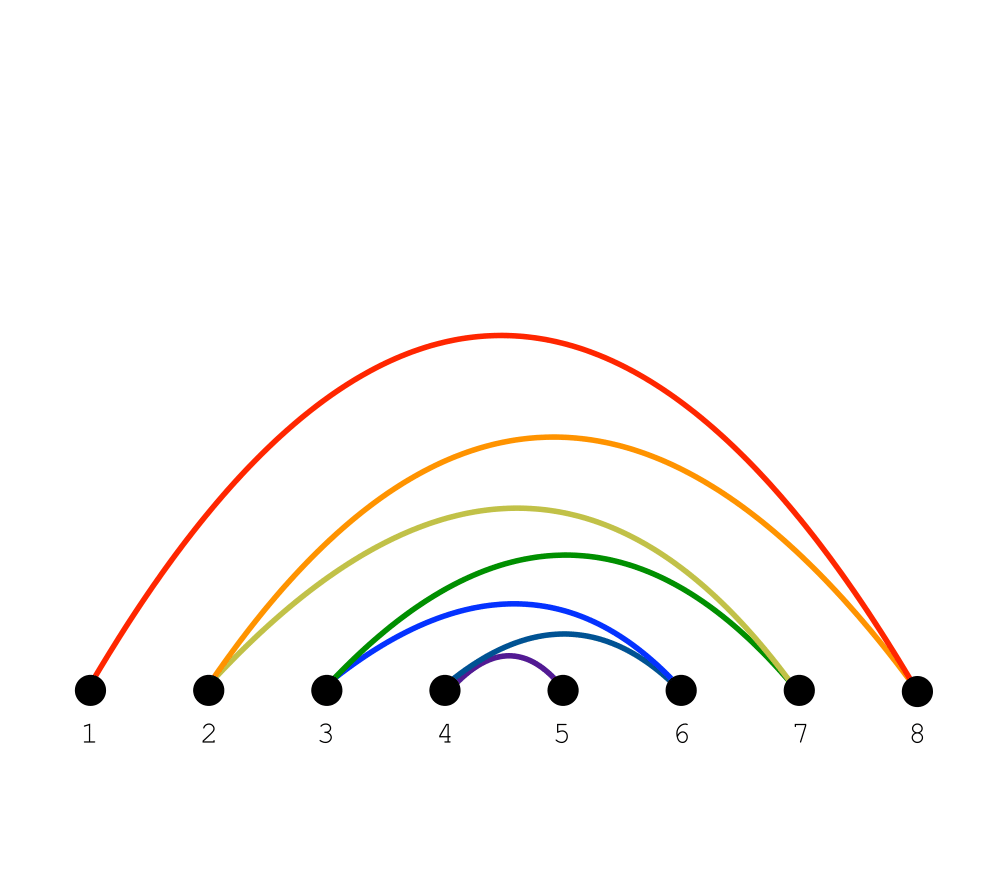
Input Description: A graph \(G=(V,E)\), representing an \(n x n\) matrix \(M\) of zero and non-zero elements.
Problem: Which permutation \(p\) of the vertices of \(V\) minimizes \(\max_{(i,j) \in E} |p(i) - p(j)|\), or equivalently the length of the longest edge when the vertices are ordered on a line.
Excerpt from The Algorithm Design Manual: Bandwidth reduction lurks as a hidden but important problem for both graphs and matrices, and it is important to see how it arises so as to properly recognize it. Applied to matrices, it permutes the rows and columns of a sparse matrix so as to minimize the distance \(b\) of any nonzero entry from the center diagonal. This is important in solving linear systems, because Gaussian elimination can be performed in \(O(n b2)\) on matrices of bandwidth \(b\). This is a big win over the general \(O(n3)\) algorithm if \(b << n\).
Bandwidth minimization on graphs arises in more subtle ways. Arranging a set of \(n\) circuit components in a line on a circuit board so as to minimize the length of the longest wire (and hence time delay) is a bandwidth problem, where each vertex of our graph corresponds to a circuit component and there is an edge for every wire linking two components.
 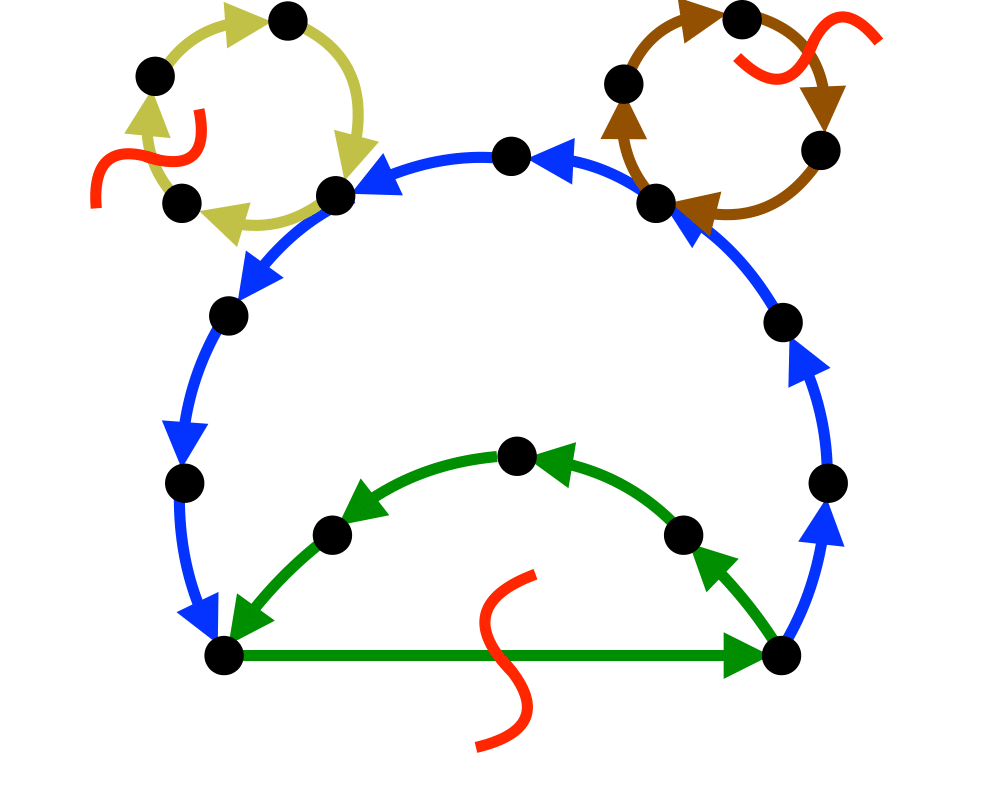 Feedback Edge/Vertex Set |
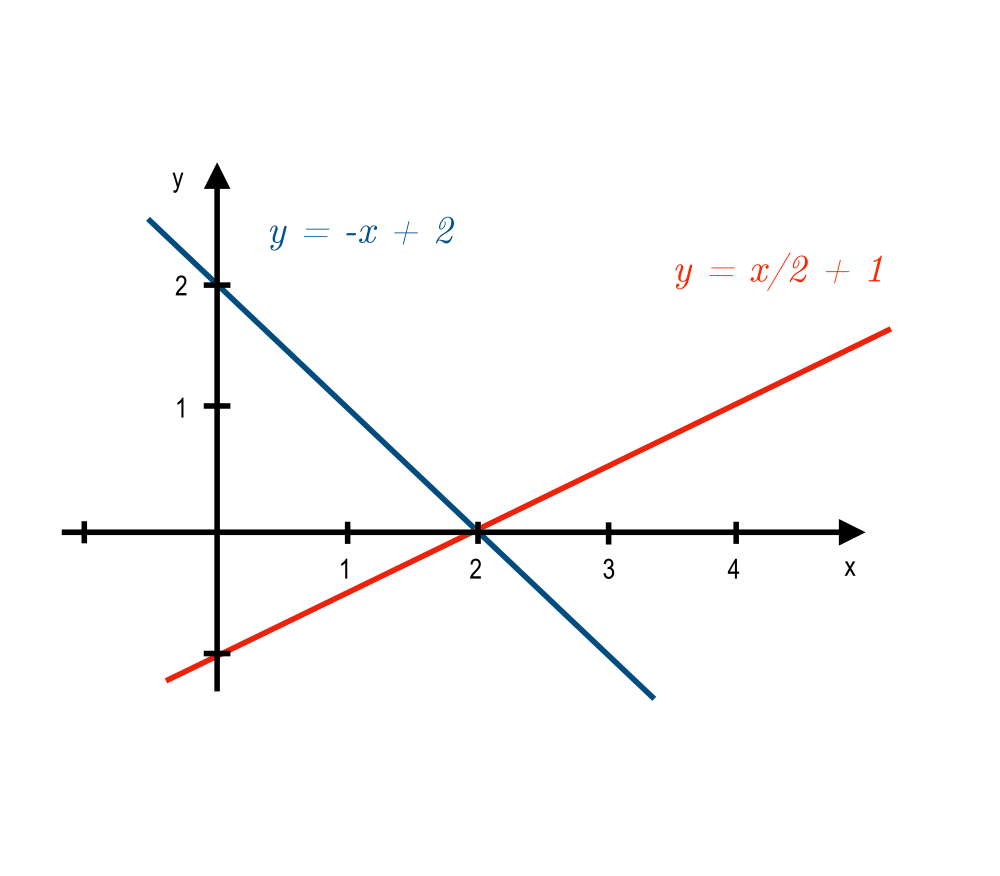 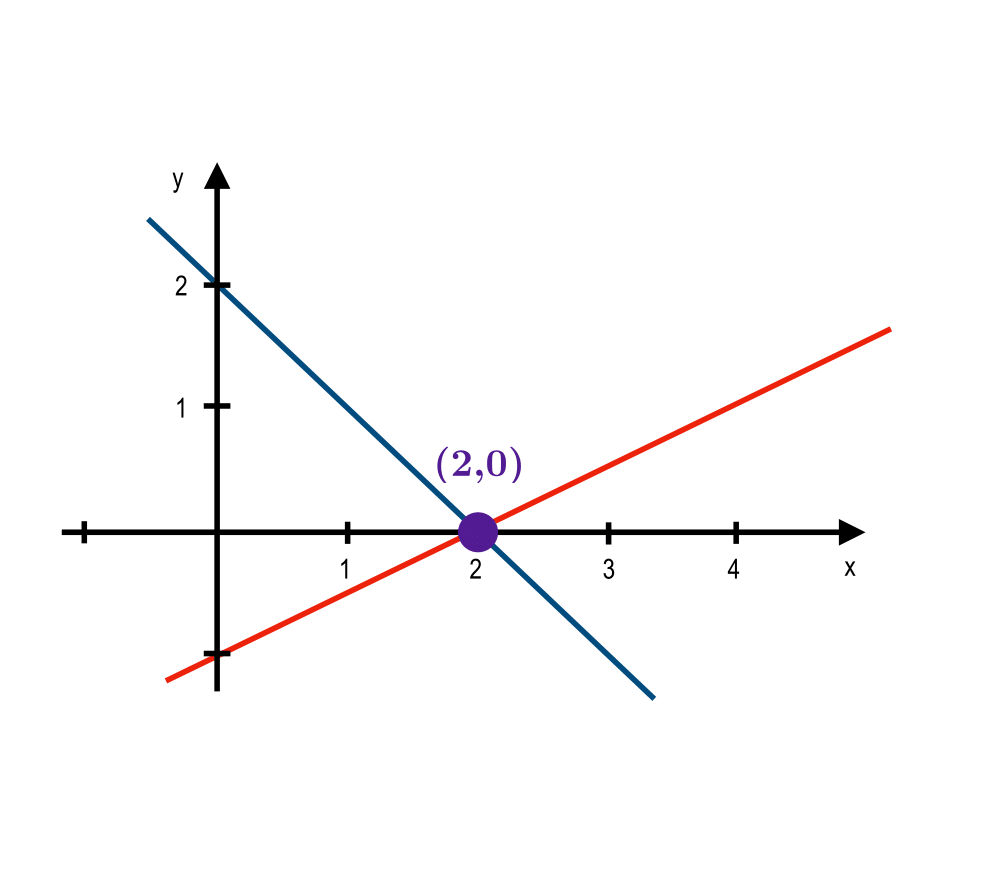 Solving Linear Equations |
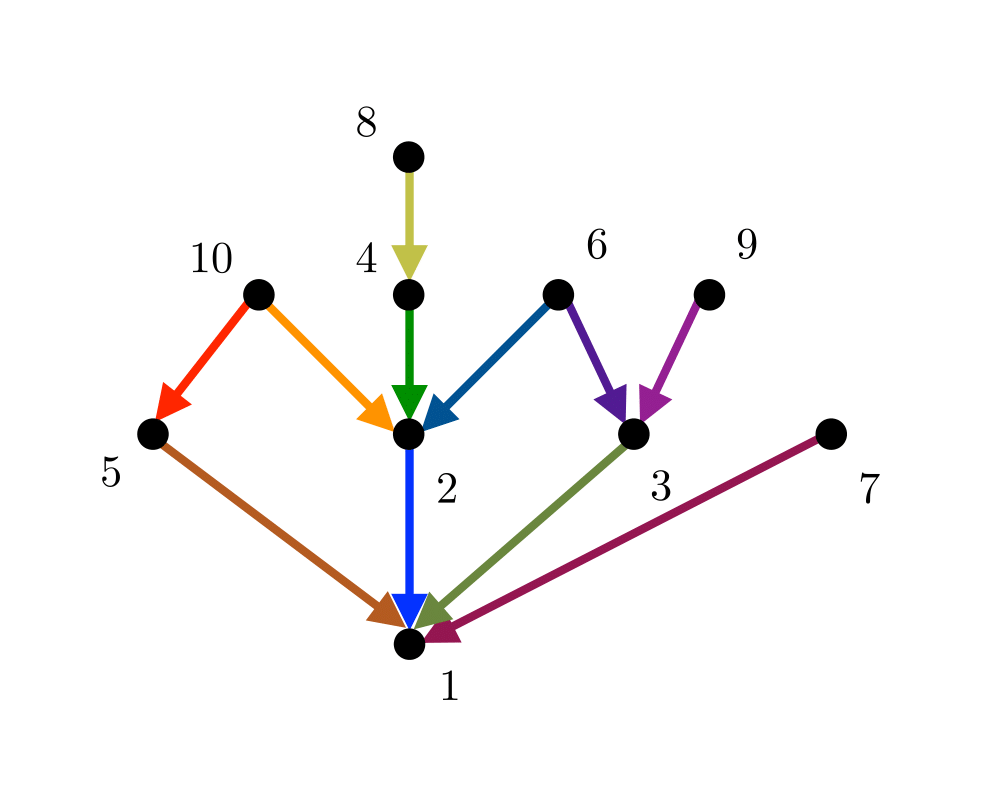  Topological Sorting |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.