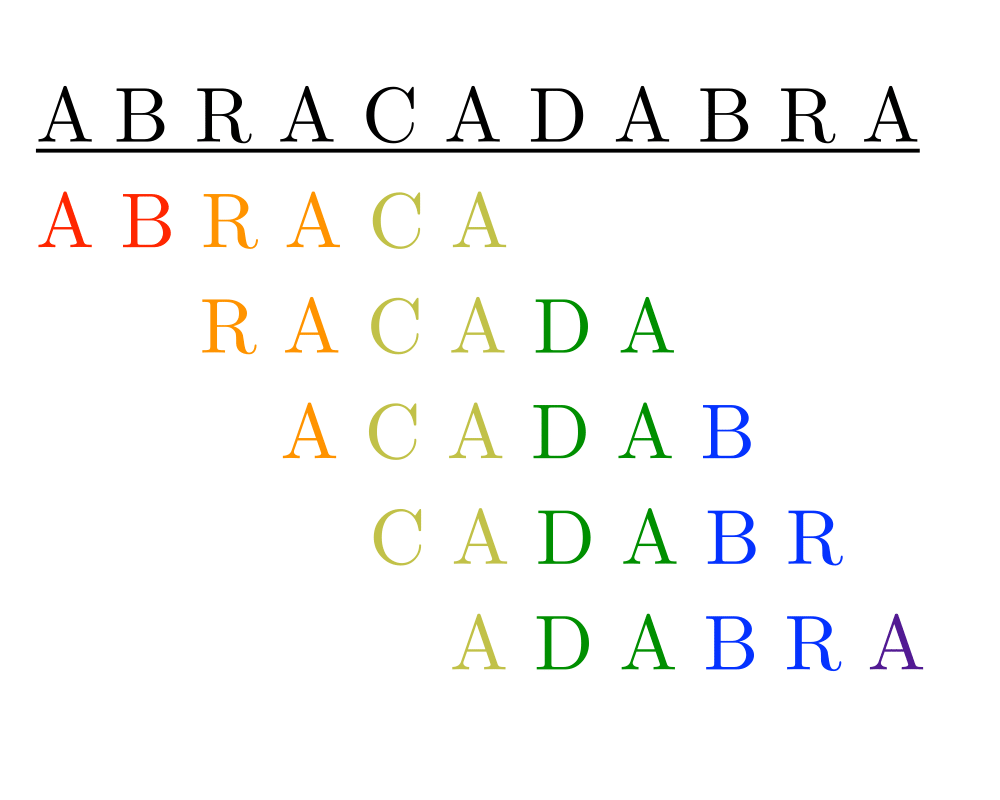 |
 |
|
|
Input Description: A set of strings \(s_1, ..., s_m\).
Problem: Find the shortest string \(S\) which contains each \(s_i\) as a substring of \(S\).
Excerpt from The Algorithm Design Manual: Shortest common superstring arises in a variety of applications, including sparse matrix compression. Suppose we have an \(n X m\) matrix with most of the elements being zero. We can partition each row into \(m/k\) runs of \(k\) elements each and construct the shortest common superstring \(S'\) of these runs. We now have reduced the problem to storing the superstring, plus an \(n X m/k\) array of pointers into the superstring denoting where each of the runs starts. Accessing a particular element \(M[i,j]\) still takes constant time, but there is a space savings when \(|S| << mn\).
| CAP (rating 9) |
Celera Assembler (rating 8) |
| superstring (rating 5) |
 Algorithms on Strings, Trees, and Sequences by Dan Gusfield |
 Introduction to Computational Biology by M. Waterman |
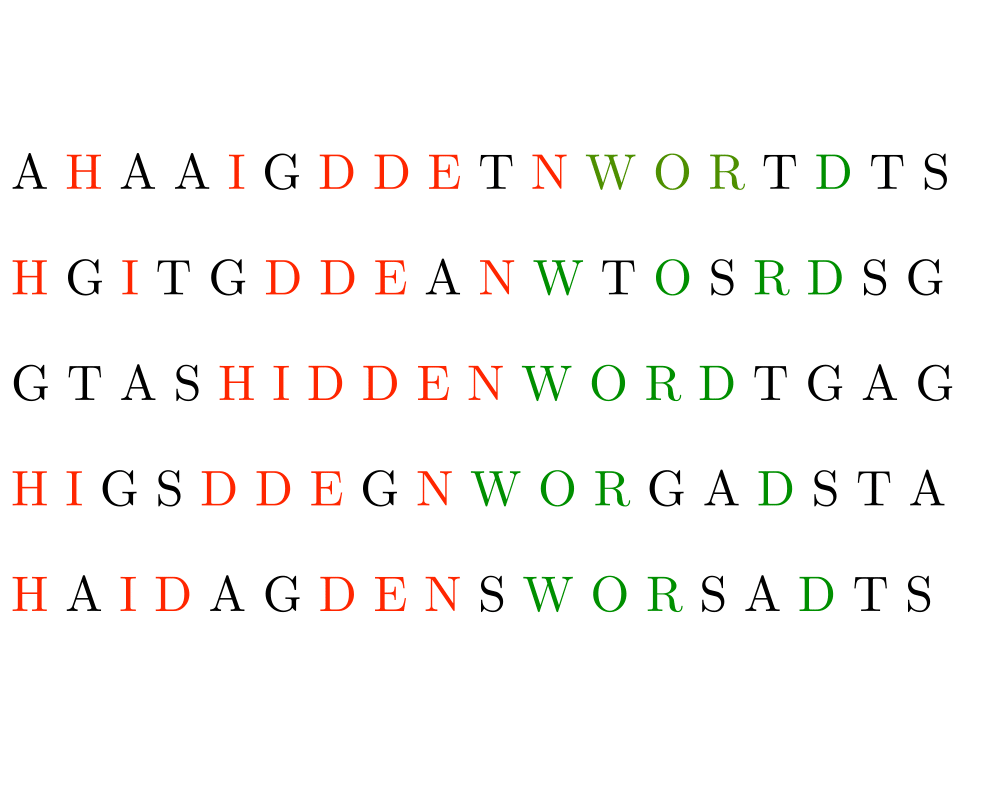  Longest Common Substring/Subsequence |
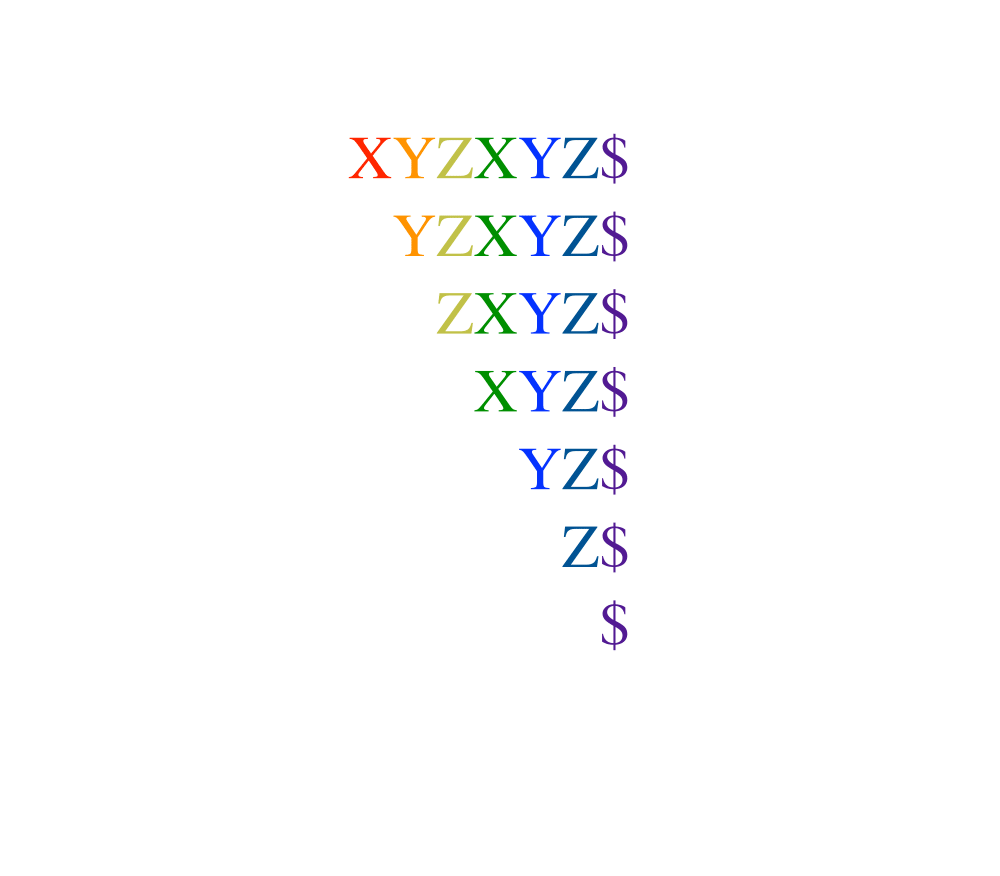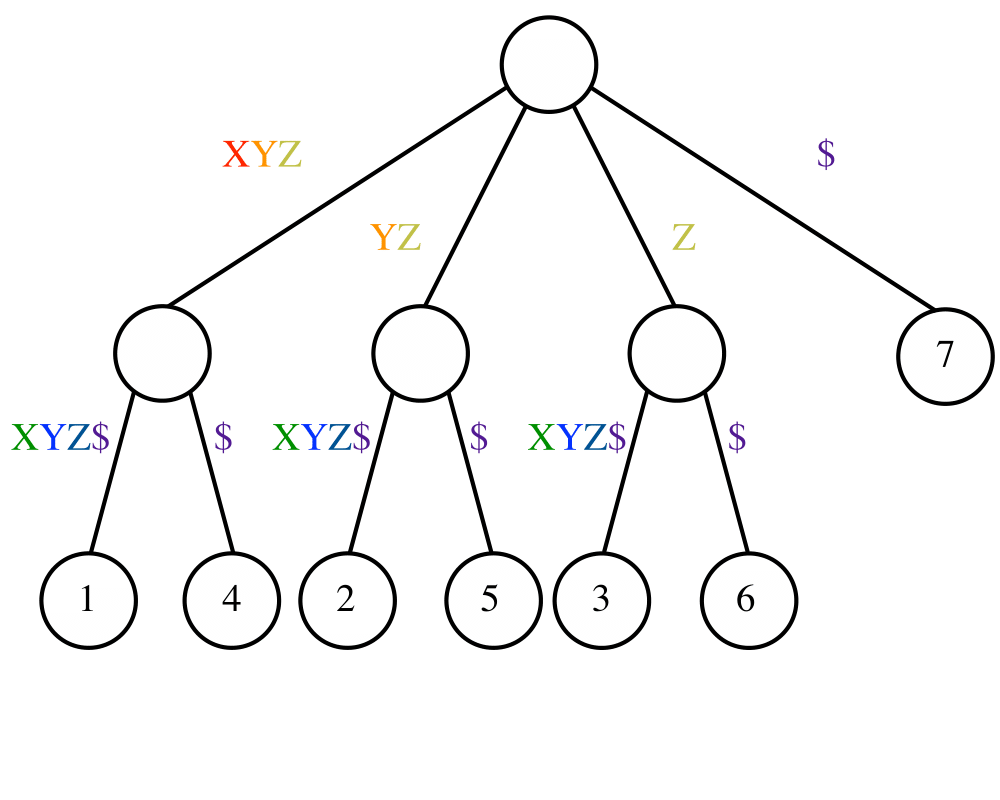  Suffix Trees and Arrays |
  Text Compression |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.