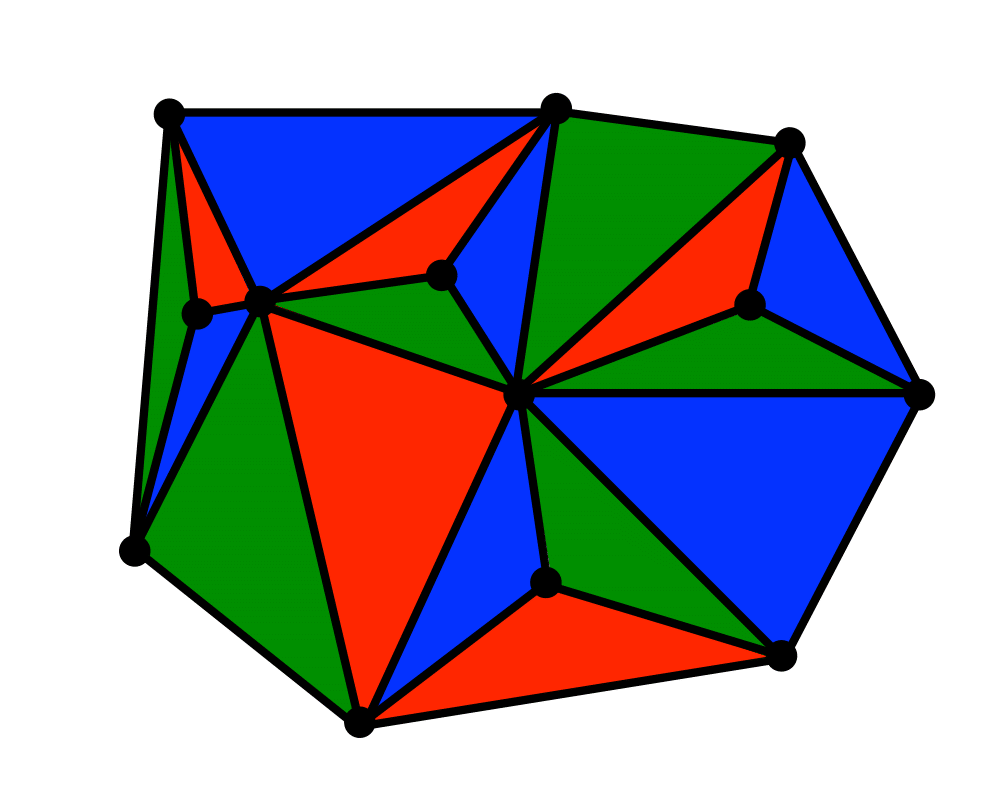
 |
 |
|
|
Input Description: A set of points, or a polyhedron
Problem: Partition the interior of the point set or polyhedron into triangles.
Excerpt from The Algorithm Design Manual: Triangulation is a fundamental problem in computational geometry, because the first step in working with complicated geometric objects is to break them into simple geometric objects. The simplest geometric objects are triangles in two dimensions, and tetrahedra in three. Classical applications of triangulation include finite element analysis and computer graphics.
A particularly interesting application of triangulation is surface or function interpolation. Suppose that we have sampled the height of a mountain at a certain number of points. How can we estimate the height at any point \(q\) in the plane? If we project the points on the plane, and then triangulate them, the triangulation completely partitions the plane into regions. We can estimate the height of \(q\) by interpolating among the three points of the triangle that contains it. Further, this triangulation and the associated height values define a surface of the mountain suitable for graphics rendering.
  Polygon Partitioning |
  Voronoi Diagrams |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
Computational Geometry : Algorithms and Applications by Mark De Berg, Marc Van Kreveld, Mark Overmars, and O. Schwartskopf
Computational Geometry in C by Joseph O'Rourke
Computational Geometry by F. Preparata and M. Shamos