 |
 |
|
|
Input Description: A deterministic finite automata \(M\).
Problem: The smallest deterministic finite automata \(M'\) such that \(M'\) behaves identically to \(M'\)
Excerpt from The Algorithm Design Manual: Problems associated with constructing and minimizing finite state machines arise repeatedly in software and hardware design applications. Finite state machines are best thought of as pattern recognizers, and minimum-size machines correspond to recognizers that require less time and space. %Space is usually the more important issue. Complicated control systems and compilers are often built using finite state machines to encode the current state and associated actions, as well as the set of possible transitions to other states. Minimizing the size of this machine minimizes its cost.
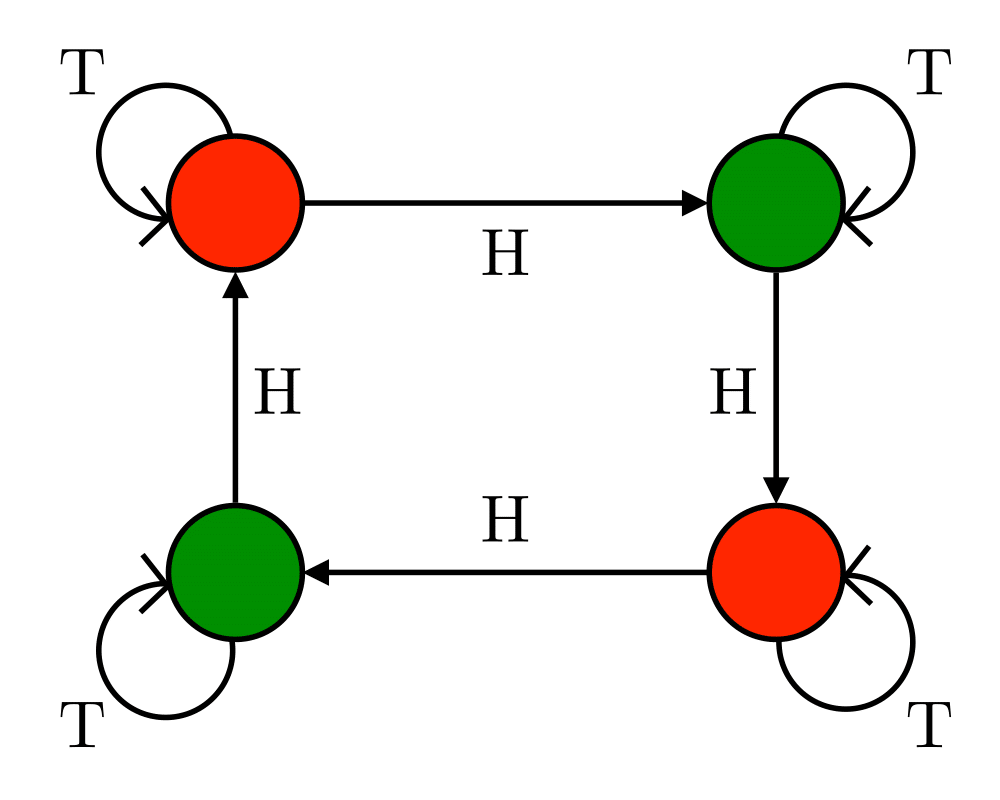
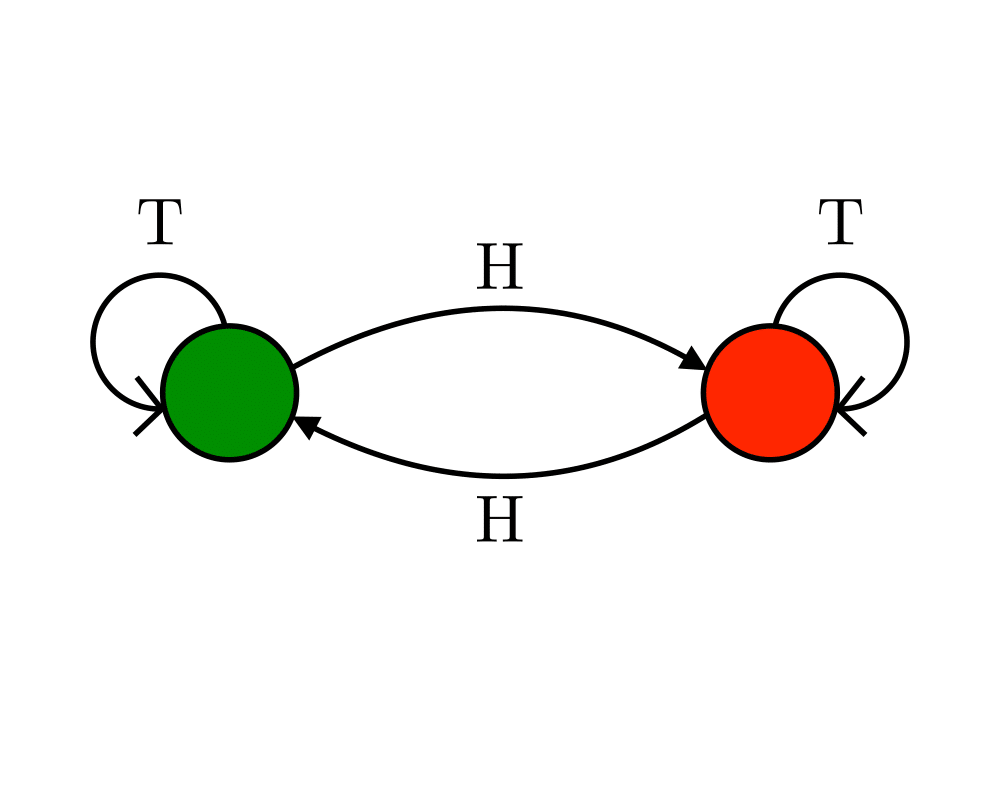
Finite state machines are best thought of as edge-labeled directed graphs, where each vertex represents one of \(n\) states and each edge a transition from one state to the other on receipt of the alphabet symbol that labels the edge. The automaton above analyzes a given sequence of coin tosses, with the dark states signifying that an even number of heads have been observed.
Practical Algorithms for Programmers by A. Binstock and J. Rex
Handbook of Algorithms and Data Structures by G. Gonnet and R. Baeza-Yates
The Design and Analysis of Computer Algorithms by A. Aho and J. Hopcroft and J. Ullman
Regular Algebra and Finite Machines by J. H. Conway
