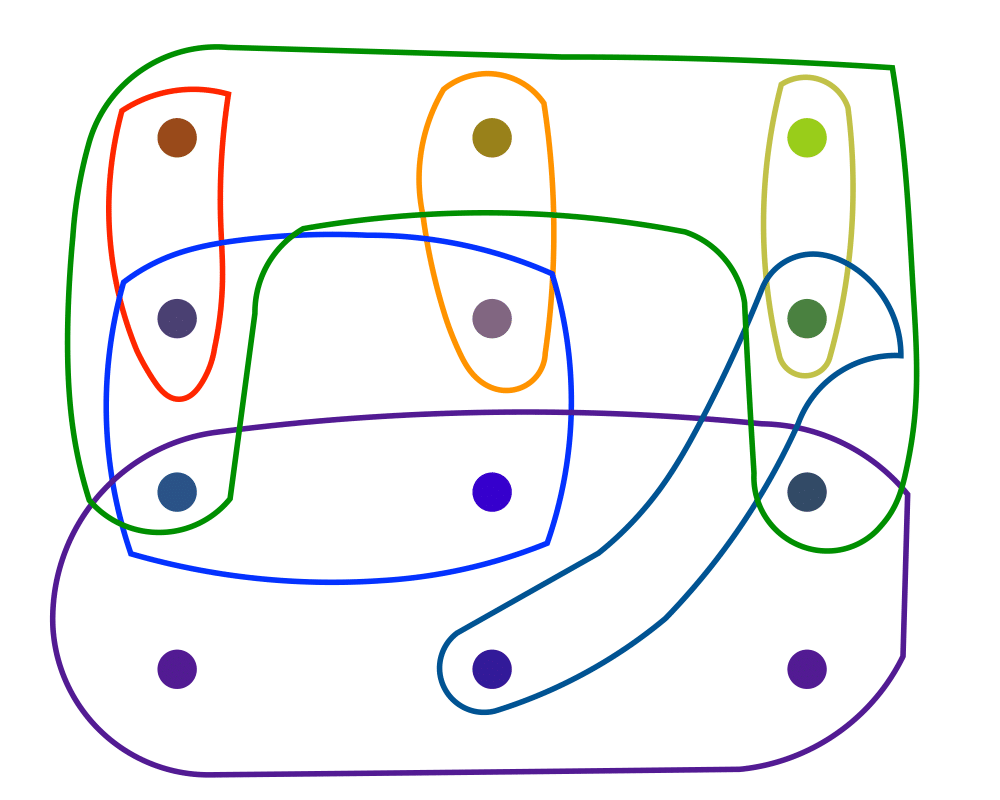
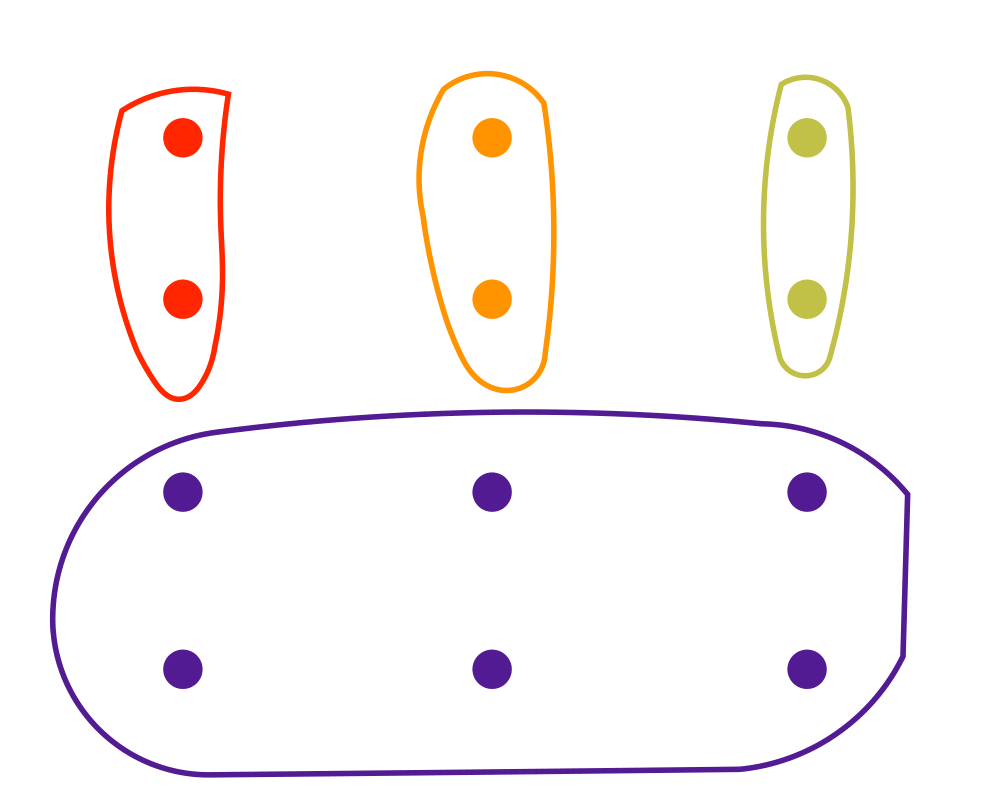
 |
 |
|
|
Input Description: A set of subsets \(S = S_1, ..., S_m\) of the universal set \(U = \{1,...,n\}\).
Problem: What is the largest number of mutually disjoint subsets from \(S\)?
Excerpt from The Algorithm Design Manual: Set packing problems arise in partitioning applications, where we need to partition elements under strong constraints on what is an allowable partition. The key feature of packing problems is that no elements are permitted to be covered by more than one set. We seek a large subset of vertices such that each edge is adjacent to at most one of the selected vertices. To model this as set packing, let the universal set consist of all edges of \(G\), and subset \(Si\) consist of all edges incident on vertex \(vi\). Any set packing corresponds to a set of vertices with no edge in common, in other words, an independent set.
Scheduling airline flight crews to airplanes is another application of set packing. Each airplane in the fleet needs to have a crew assigned to it, consisting of a pilot, copilot, and navigator. There are constraints on the composition of possible crews, based on their training to fly different types of aircraft, as well as any personality conflicts. Given all possible crew and plane combinations, each represented by a subset of items, we need an assignment such that each plane and each person is in exactly one chosen combination. After all, the same person cannot be on two different planes, and every plane needs a crew. We need a perfect packing given the subset constraints.
| optimal_partition (rating 6) |
setcover (rating 6) |
| SetCoverPy (rating 6) |
SYMPHONY (rating 6) |
| Discrete Optimization Methods (rating 6) |
spp_tabu_solver (rating 4) |
 Discrete Optimization Algorithms with Pascal Programs by M. Syslo and N. Deo and J. Kowalik |
