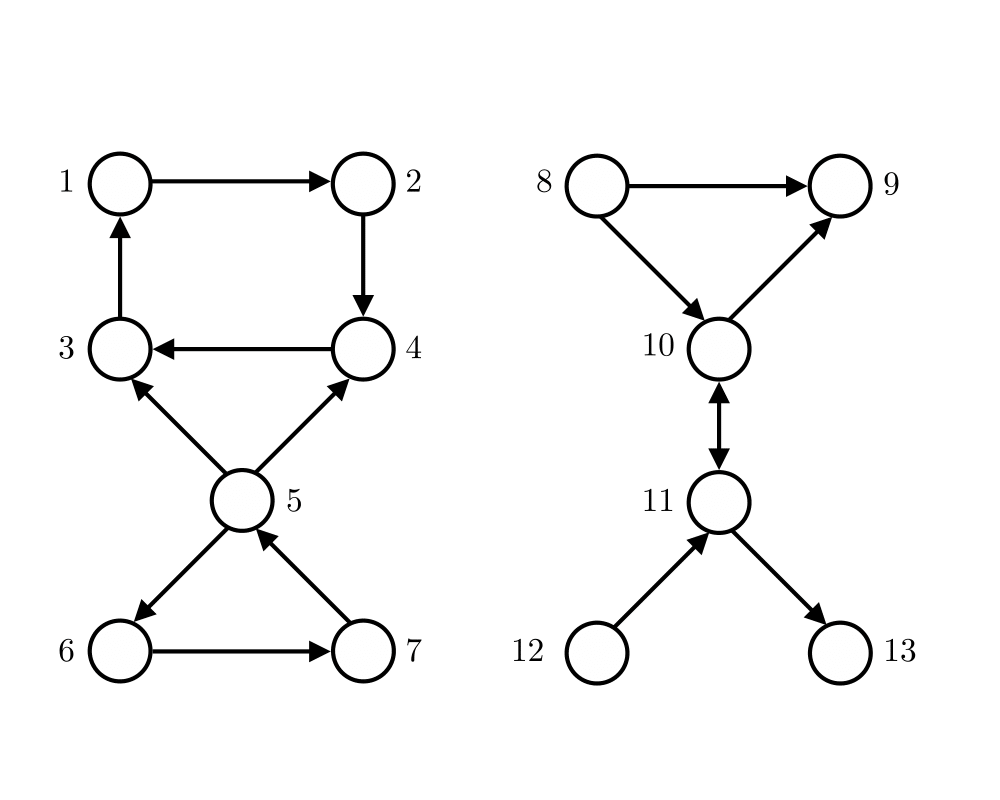
 |
 |
|
|
Input Description: A directed or undirected graph \(G\). A start vertex \(s\).
Problem: Traverse each edge and vertex of the connected component containing \(s\).
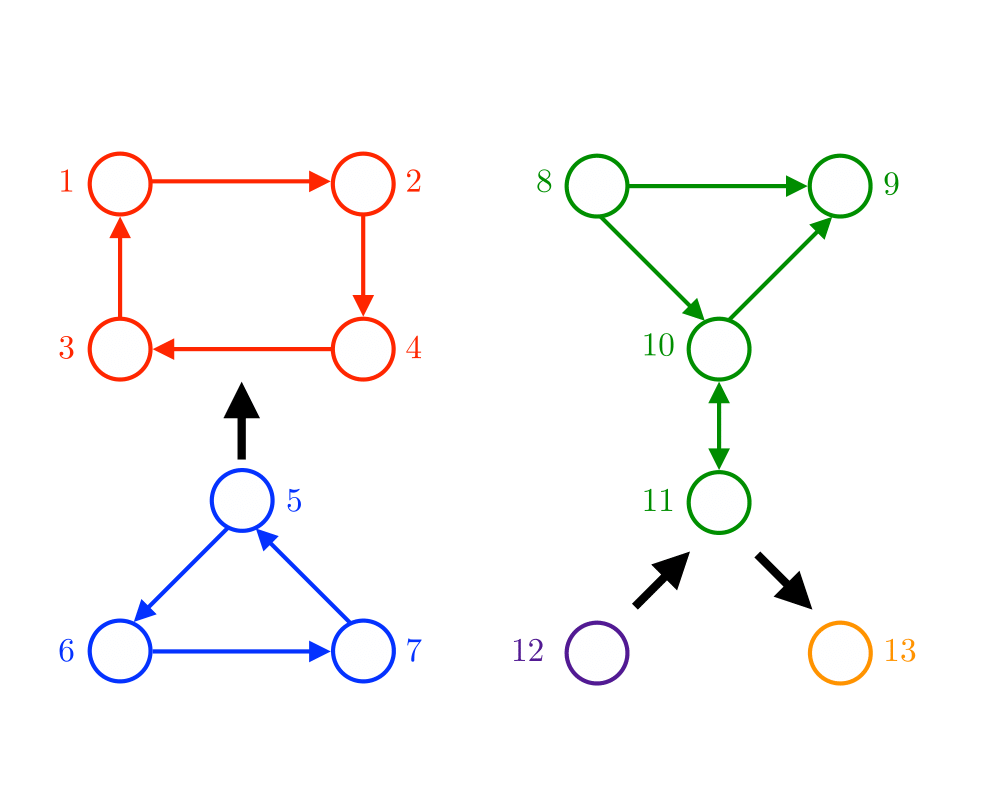
Excerpt from The Algorithm Design Manual: The connected components of a graph represent, in grossest terms, the pieces of the graph. Two vertices are in the same component of \(G\) if and only if there is some path between them.
Finding connected components is at the heart of many graph applications. For example, consider the problem of identifying clusters in a set of items. We can represent each item by a vertex and add an edge between each pair of items that are deemed ``similar.'' The connected components of this graph correspond to different classes of items.
Testing whether a graph is connected is an essential preprocessing step for every graph algorithm. Such tests can be performed so quickly and easily that you should always verify that your input graph is connected, even when you know it has to be. Subtle, difficult-to-detect bugs often result when your algorithm is run only on one component of a disconnected graph.
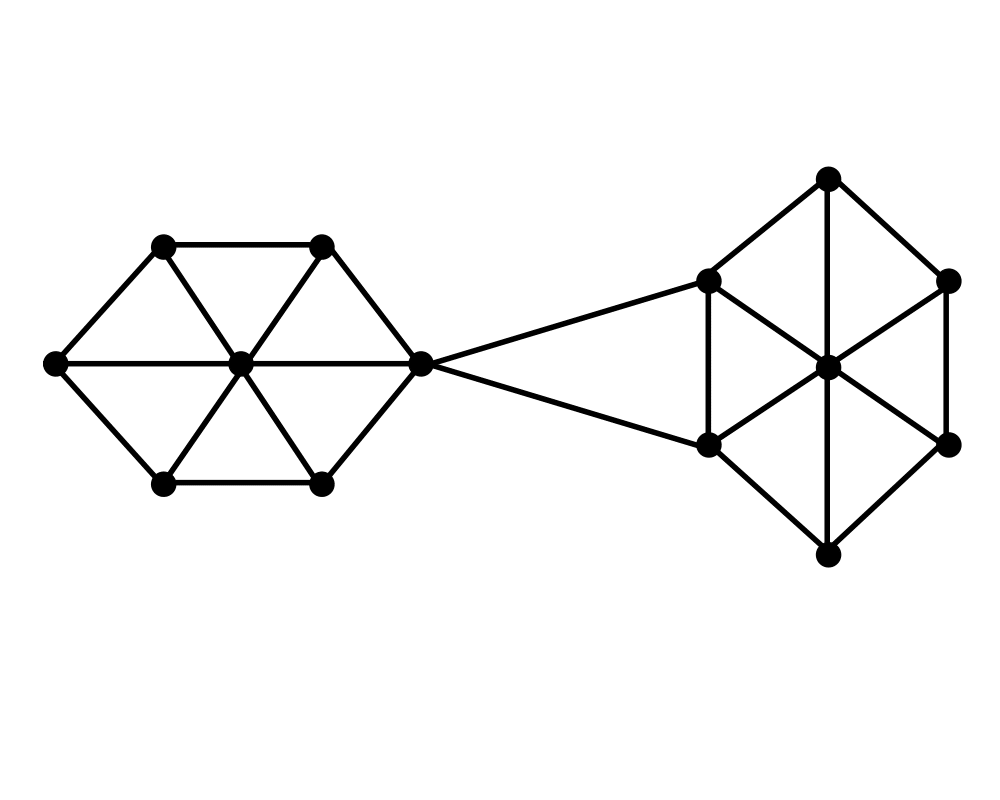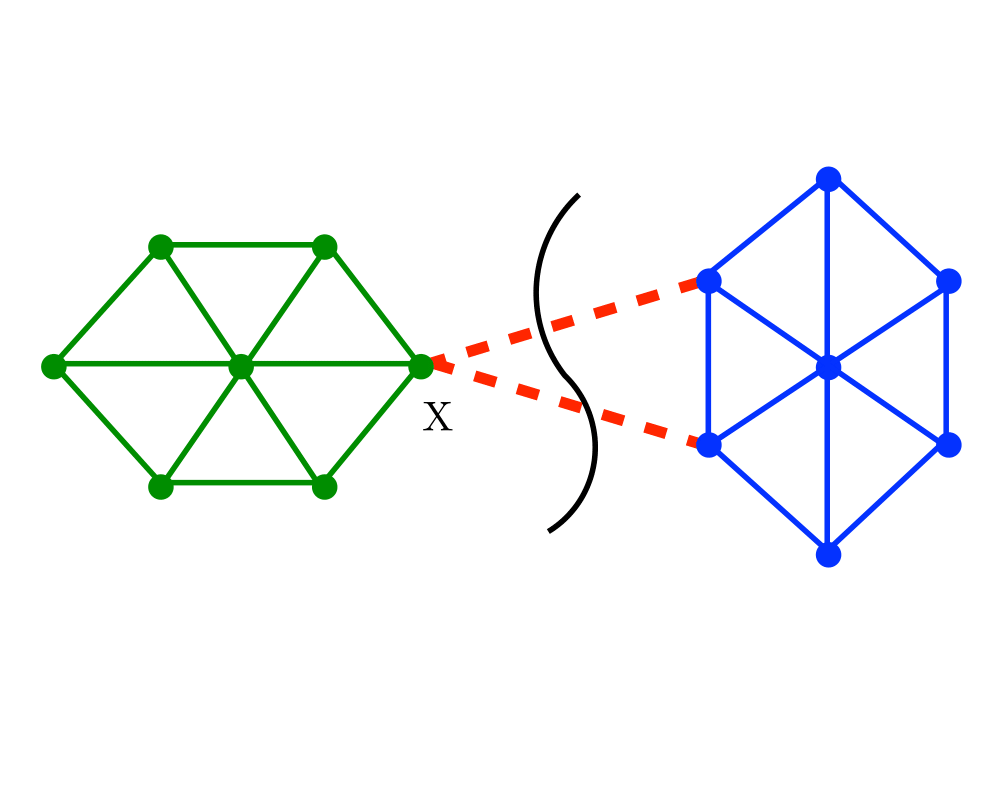  Edge and Vertex Connectivity |
  Shortest Path |
  Transitive Closure and Reduction |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
Introduction to Algorithms by T. Cormen and C. Leiserson and R. Rivest and C. Stein
Computer Algorithms by S. Baase
Data Structures and Algorithms by A. Aho and J. Hopcroft and J. Ullman
Graph Algorithms by S. Even
Recreations Mathematiques by E. Lucas