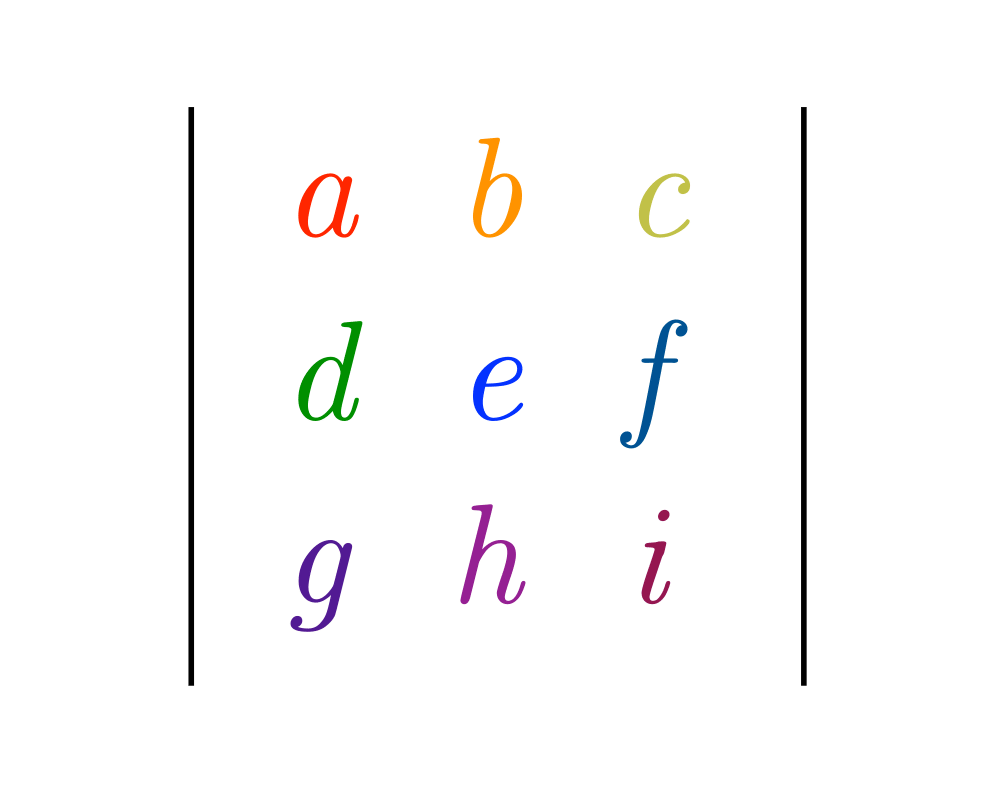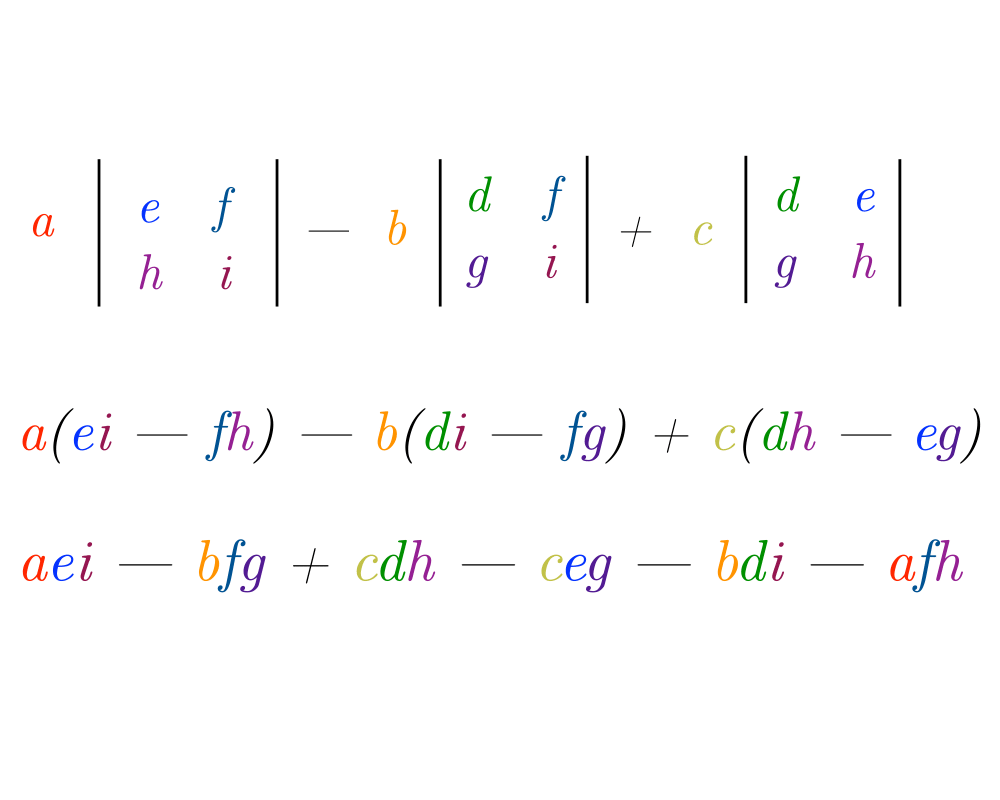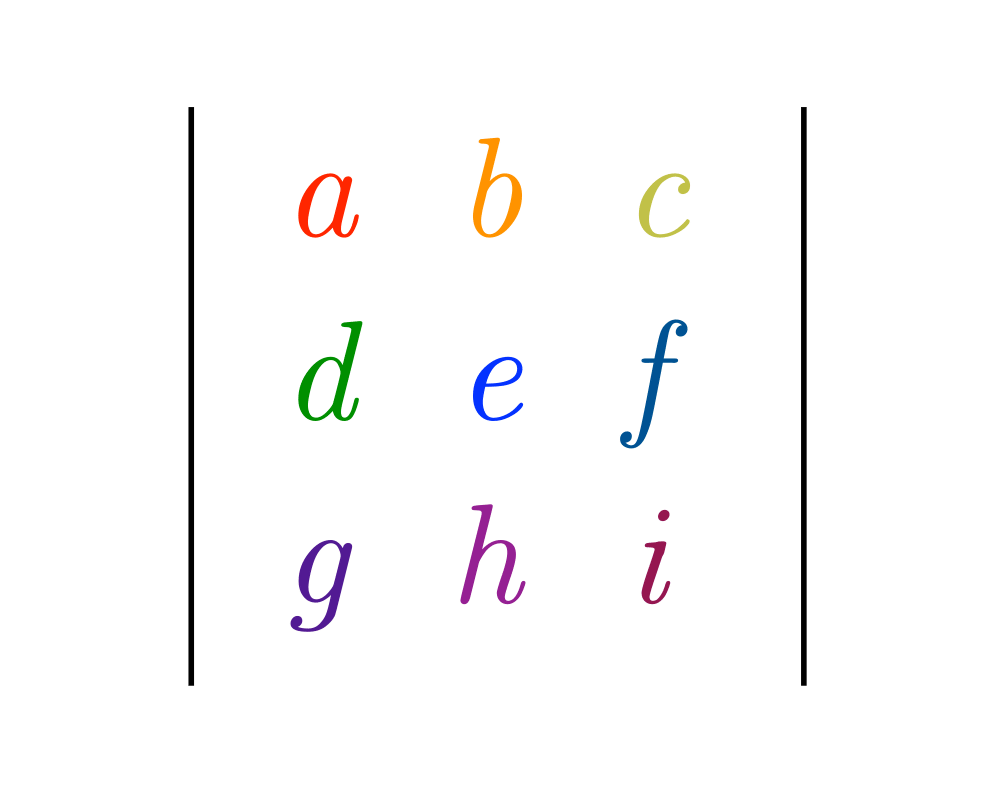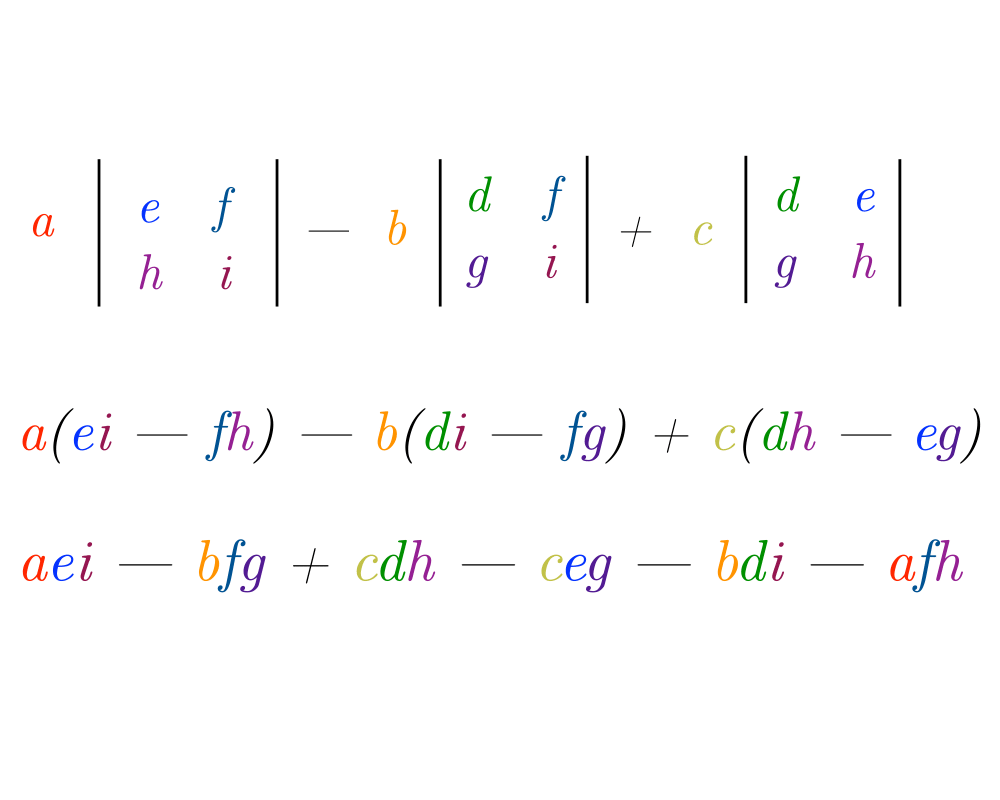Input

Output

Input Description: An \(n x n\) matrix \(M\).
Problem: What is the determinant \(|M|\) or the permanent \(Perm(M)\) for matrix \(m\)?

Excerpt from The Algorithm Design Manual: Determinants of matrices provide a clean and useful abstraction in linear algebra that can used to solve a variety of problems:

• Testing whether a matrix is singular, meaning that the matrix does not have an inverse. A matrix \(M\) is singular iff \(|M| = 0\).
• Testing whether a set of \(d\) points lies on a plane in fewer than \(d\) dimensions. If so, the system of equations they define is singular, so \(|M| = 0\).
• Testing whether a point lies to the left or right of a line or plane. This problem reduces to testing whether the sign of a determinant is positive or negative.
• Computing the area or volume of a triangle, tetrahedron, or other simplicial complex. These quantities are a function of the magnitude of the determinant.

A closely related function, called the permanent, arises often in combinatorial problems. For example, the permanent of the adjacency matrix of a graph \(G\) counts the number of perfect matchings in \(G\).

Implementations

LINPACK (rating 10)	JScience (rating 9)
Barvinok 1 (rating 8)	Barvinok 2 (rating 8)
HODLR (rating 6)	Nijenhuis and Wilf (rating 5)

Recommended Books

Matrix Computations by Gene H. Golub and Charles F. Van Loan	Numerical Recipes in Fortran 90 by William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery	Numerical Recipes in Fortran 77 by William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery
Numerical Recipes in Pascal by William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery	Numerical Recipes in C by William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery	Data Structures and Algorithms by A. Aho and J. Hopcroft and J. Ullman
Permanents by H. Minc	Combinatorial Algorithms for Computers and Calculators by A. Nijenhuis and H. Wilf	A survey of modern algebra by G. Birkhoff and S. MacLane

Related Problems

Robust Geometric Primitives

Solving Linear Equations

Matching

As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.