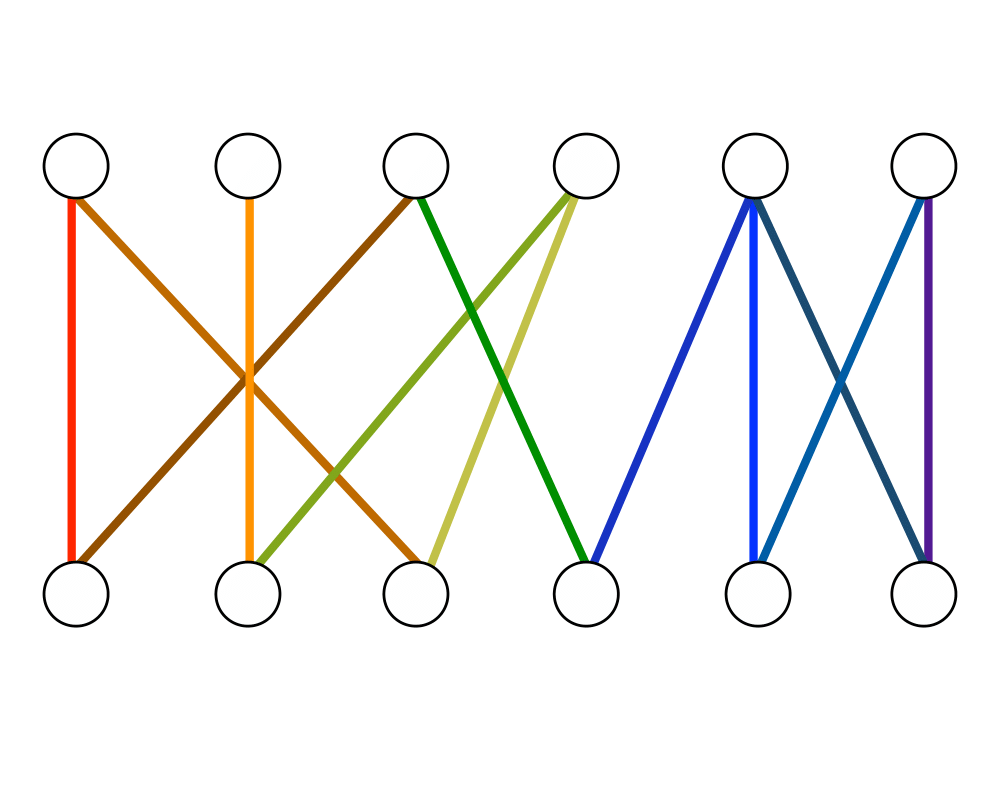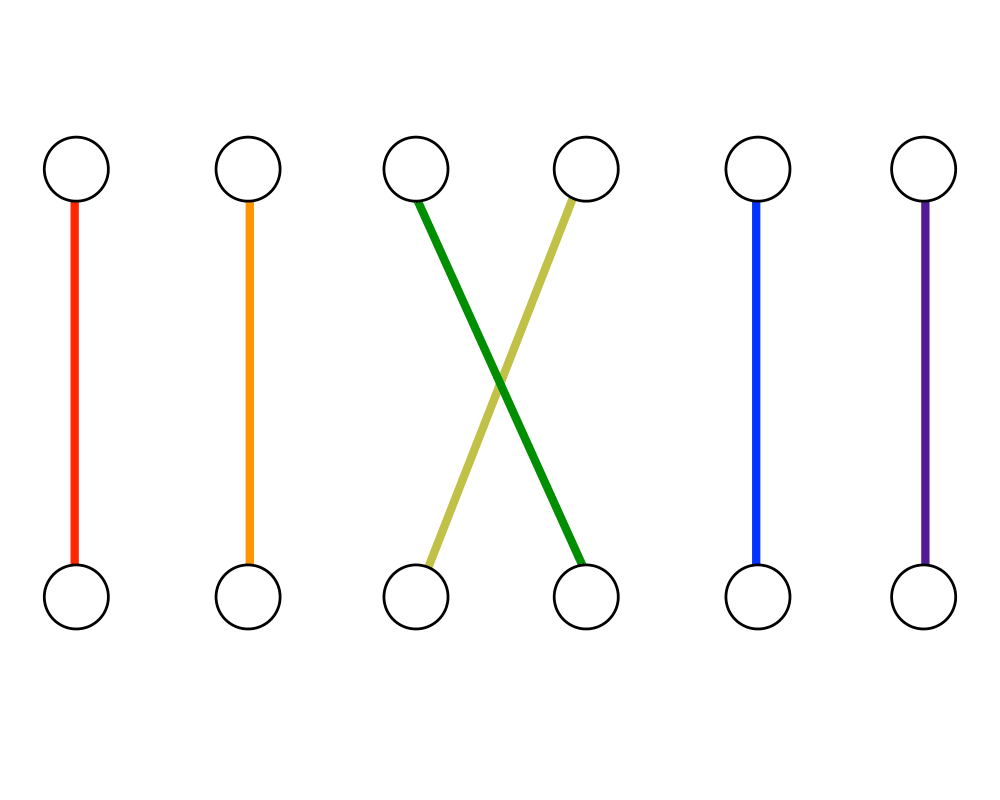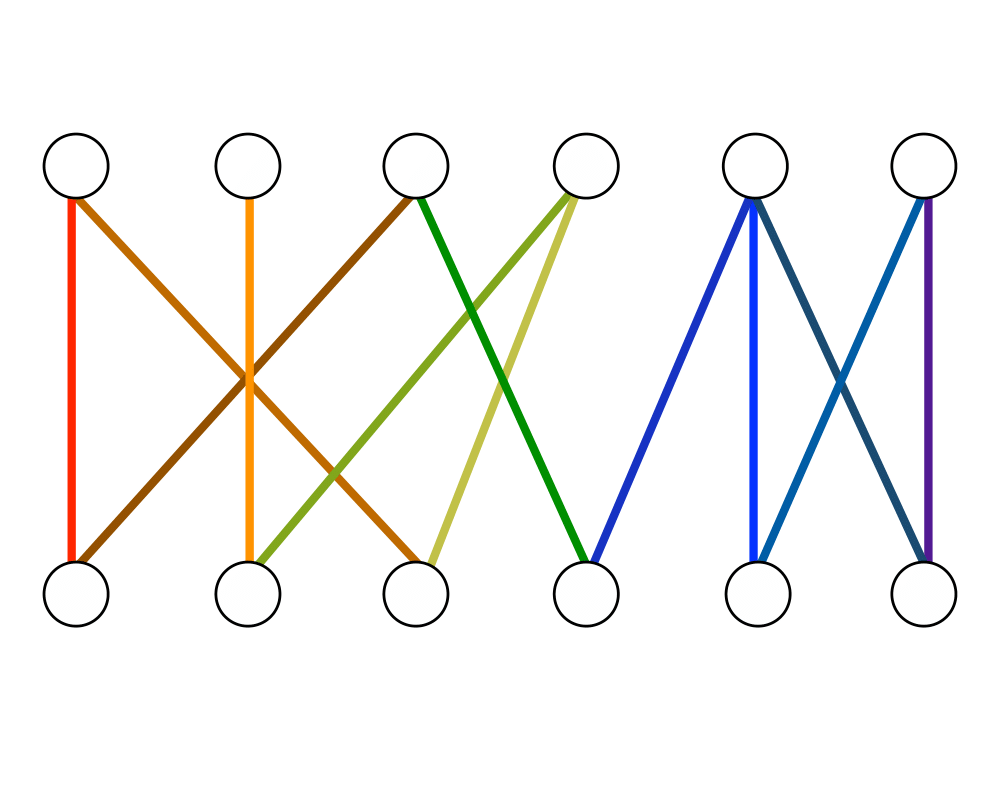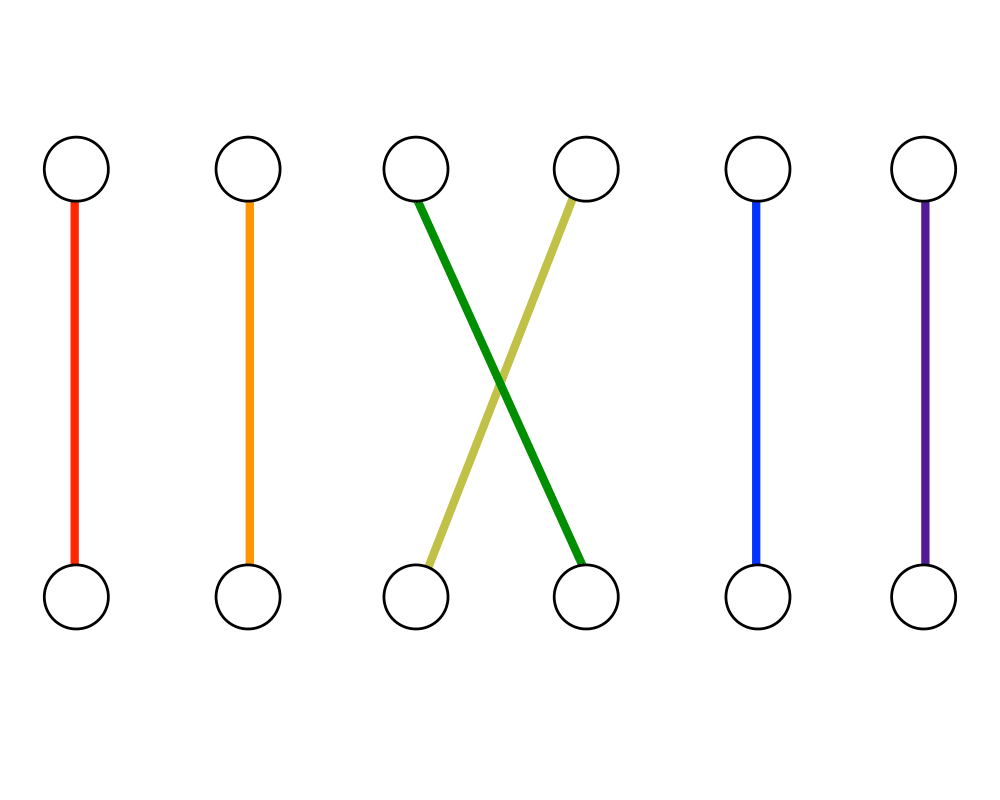 |
 |
|
|
Input Description: A (weighted) graph \(G=(V,E)\).
Problem: Find the largest size set of edges \(S \in E\) such that each vertex in \(V\) is incident to at most one edge of \(S\).
Excerpt from The Algorithm Design Manual: Consider a set of employees, each of whom is capable of doing some subset of the tasks that must be performed. We seek to find an assignment of employees to tasks such that each task is assigned to a unique employee. Each mapping between an employee and a task they can handle defines an edge, so what we need is a set of edges with no employee or job in common, i.e. a matching.
Efficient algorithms for constructing matchings are based on constructing augmenting paths in graphs. Given a (partial) matching \(M\) in a graph \(G\), an augmenting path \(P\) is a path of edges where every odd-numbered edge (including the first and last edge) is not in \(M\), while every even-numbered edge is. Further, the first and last vertices must not be already in \(M\). By deleting the even-numbered edges of \(P\) from \(M\) and replacing them with the odd-numbered edges of \(P\), we enlarge the size of the matching by one edge. Berge's theorem states that a matching is maximum if and only if it does not contain any augmenting path. Therefore, we can construct maximum-cardinality matchings by searching for augmenting paths and stopping when none exist.
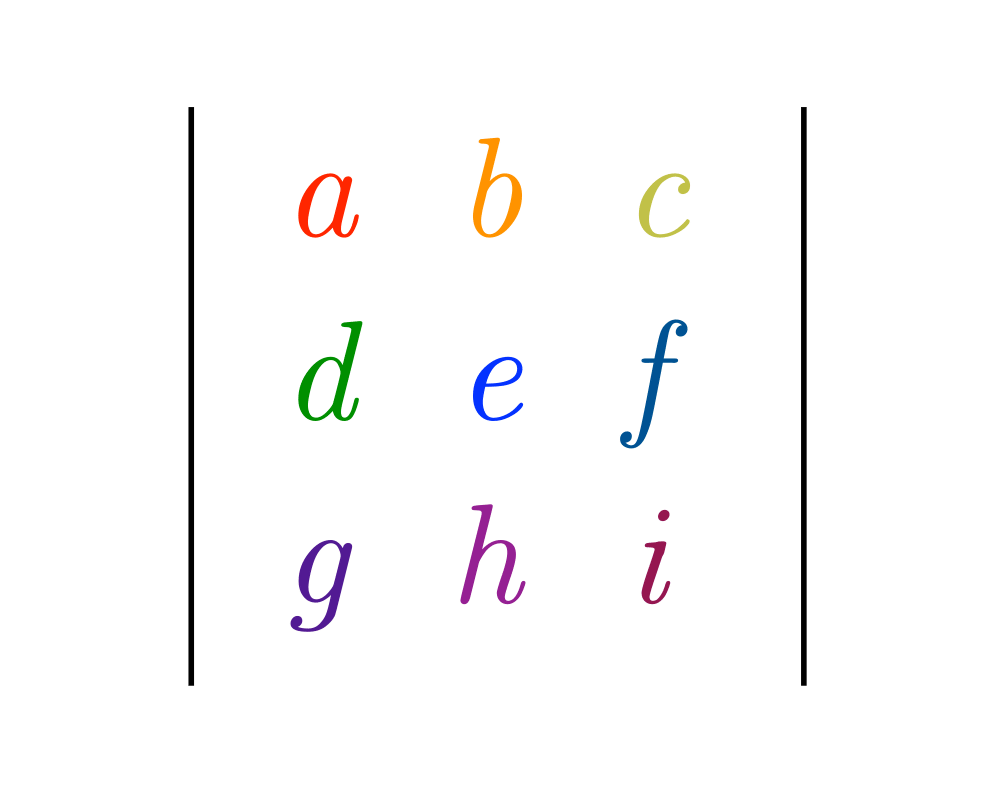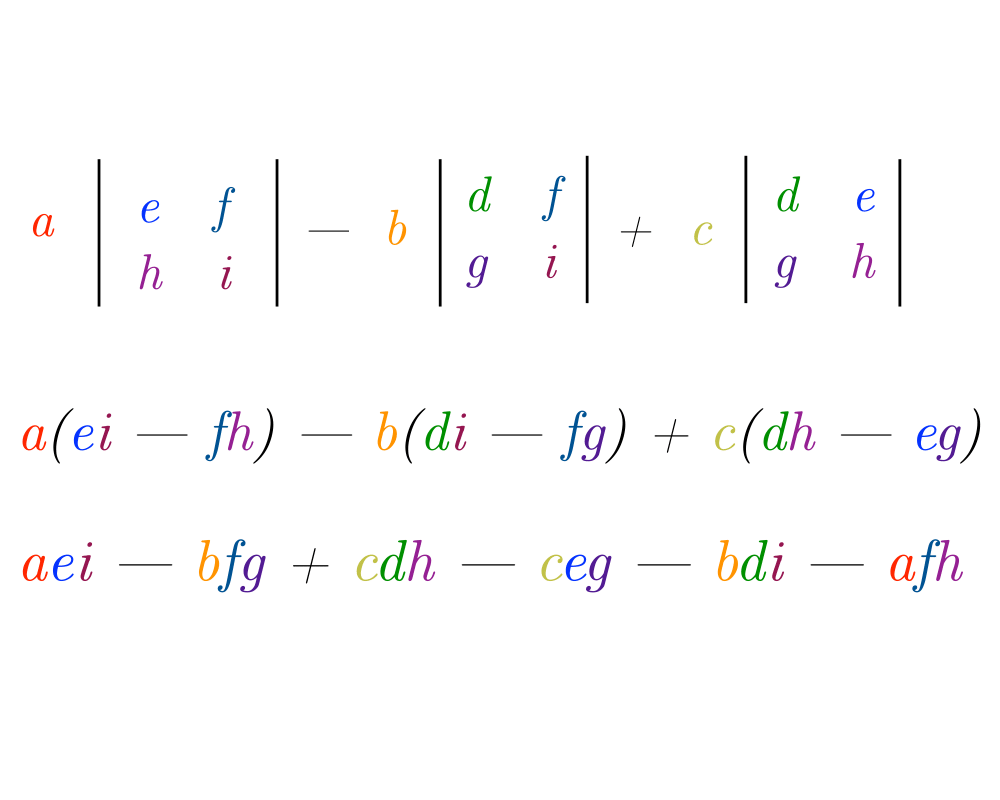  Determinants and Permanents |
  Eulerian Cycle/Chinese Postman |
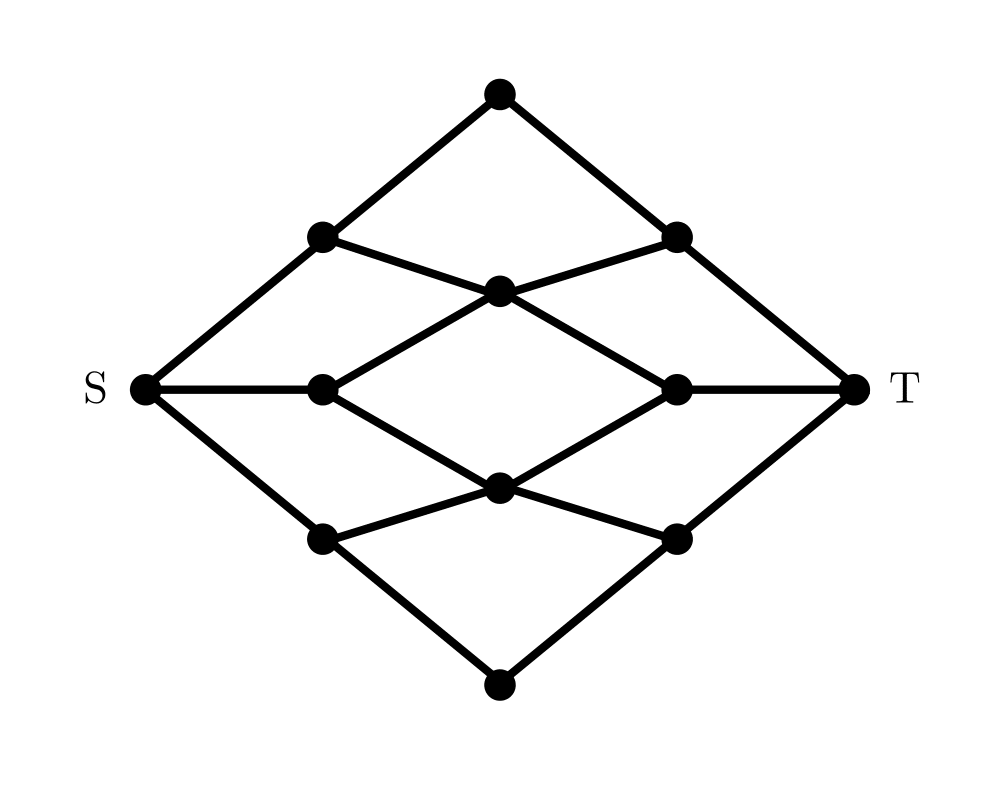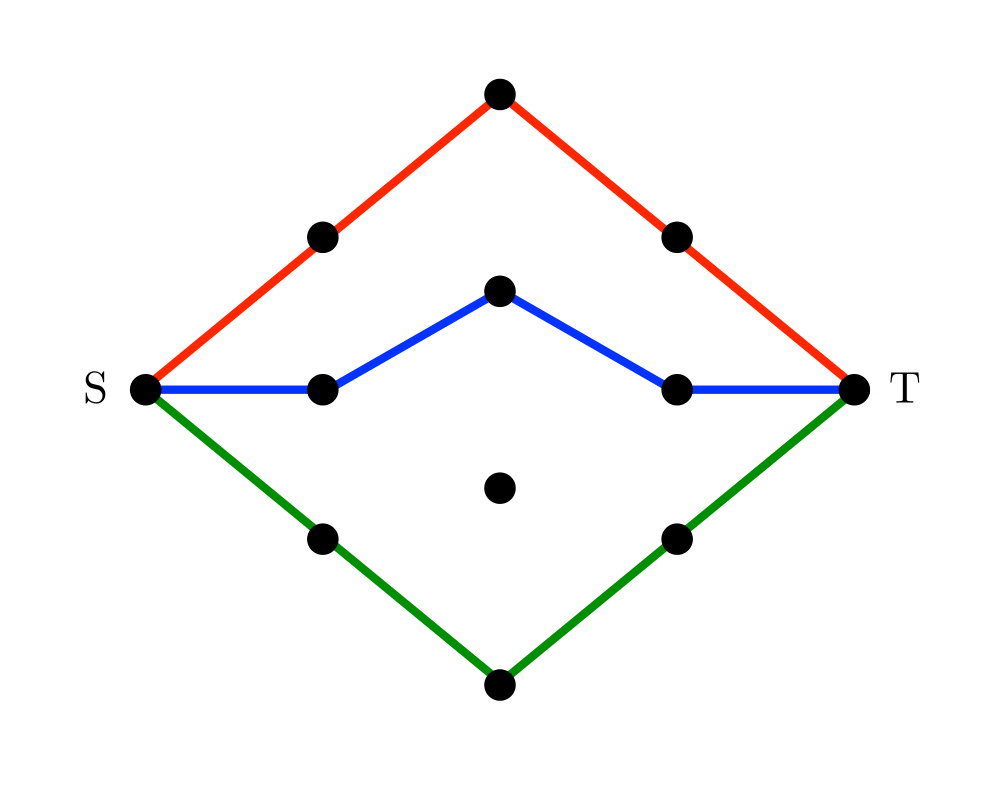  Network Flow |
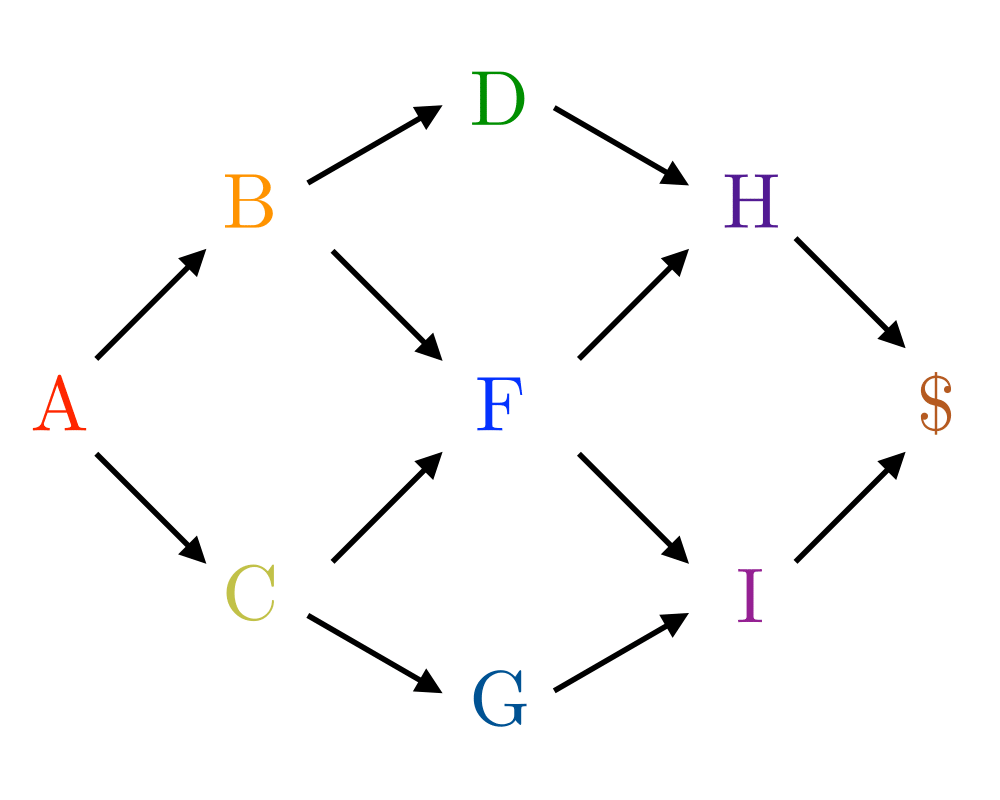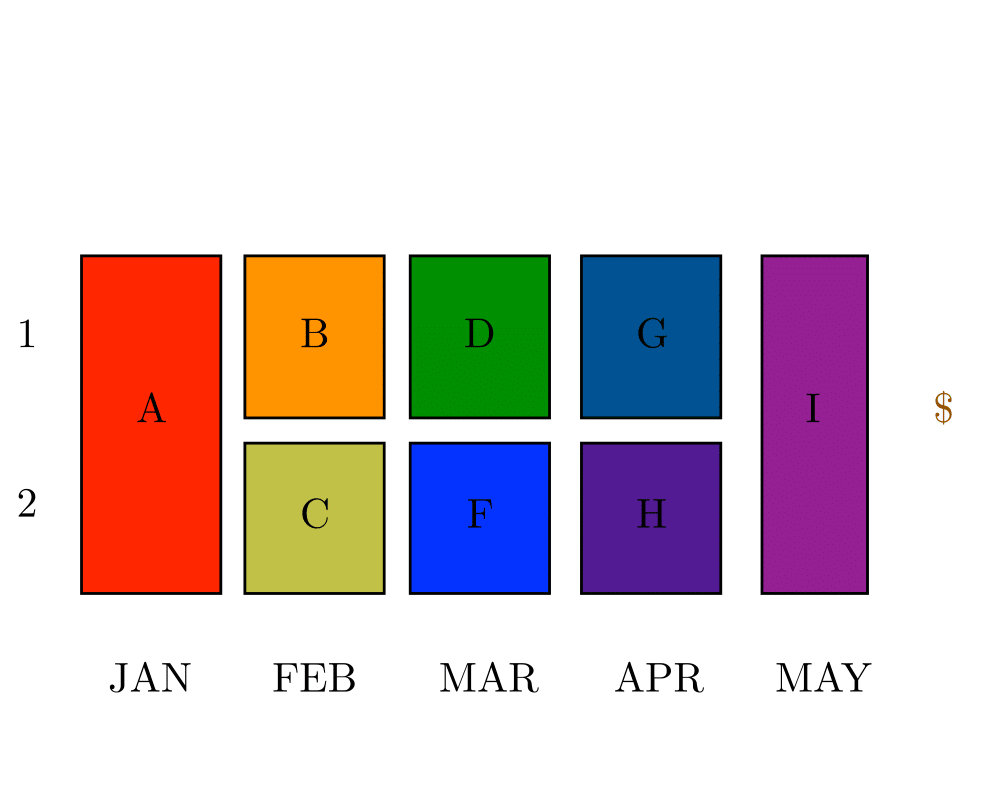  Job Scheduling |
  Set Cover |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
.jpg)
Algorithms in Java, Third Edition (Parts 1-4) by Robert Sedgewick and Michael Schidlowsky
Network Flows : Theory, Algorithms, and Applications by Ravindra K. Ahuja, Thomas L. Magnanti, and James B. Orlin
Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica by S. Pemmaraju and S. Skiena
Introduction to Algorithms by T. Cormen and C. Leiserson and R. Rivest and C. Stein
The Stable Marriage Problem: structure and algorithms by D. Gusfield and R. Irving
Matching Theory by L. Lovasz
Data Structures and Network Algorithms by R. Tarjan
Combinatorial Optimization: Algorithms and Complexity by C. Papadimitriou and K. Steiglitz