Input

Output

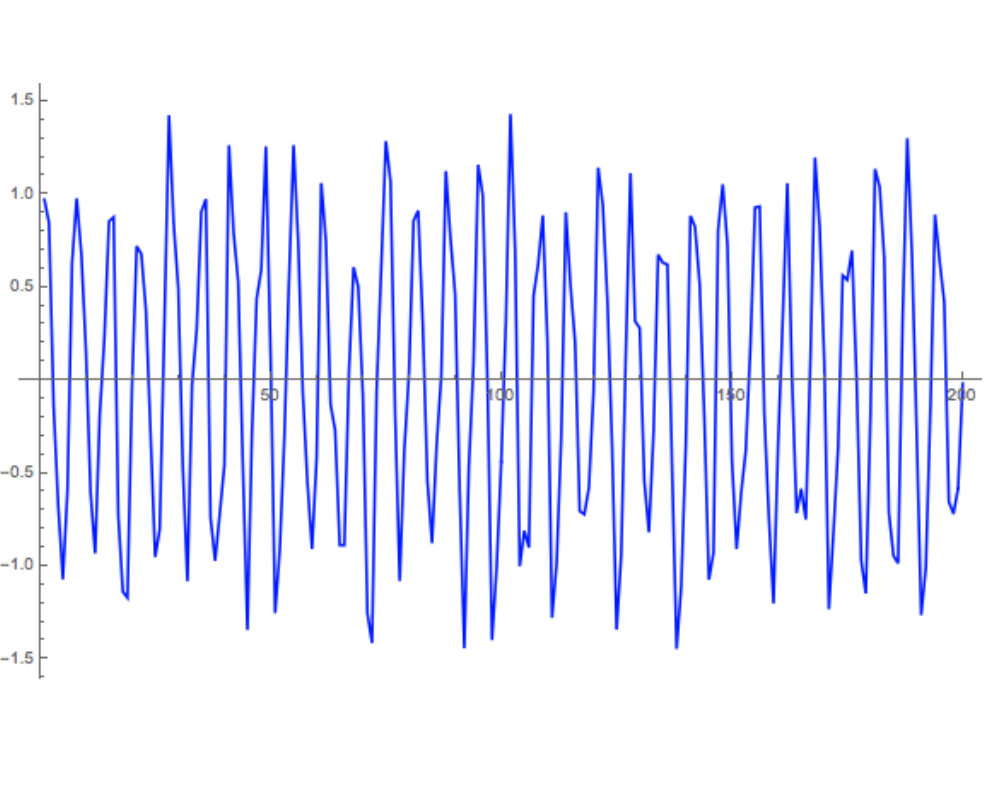
Input Description: A sequence of \(n\) real or complex values \(h_i\), \(0 \leq i \leq n-1\), sampled at uniform intervals from a function \(h\).
Problem: The discrete Fourier transform \(H\) of \(h\), \(H_m = \sum_{k=0}^{n-1} h_k e^{2 \pi i k m / n}\), \(0 \leq m \leq n-1\).

Excerpt from The Algorithm Design Manual: Although computer scientists tend to be relatively unfamiliar with Fourier transforms, electrical engineers and signal processors eat them for breakfast. Functionally, Fourier transforms provide a way to convert samples of a standard time-series into the ``frequency domain''. This provides a ``dual'' representation of the function, in which certain operations become easier than in the time domain. Applications of Fourier transforms include:

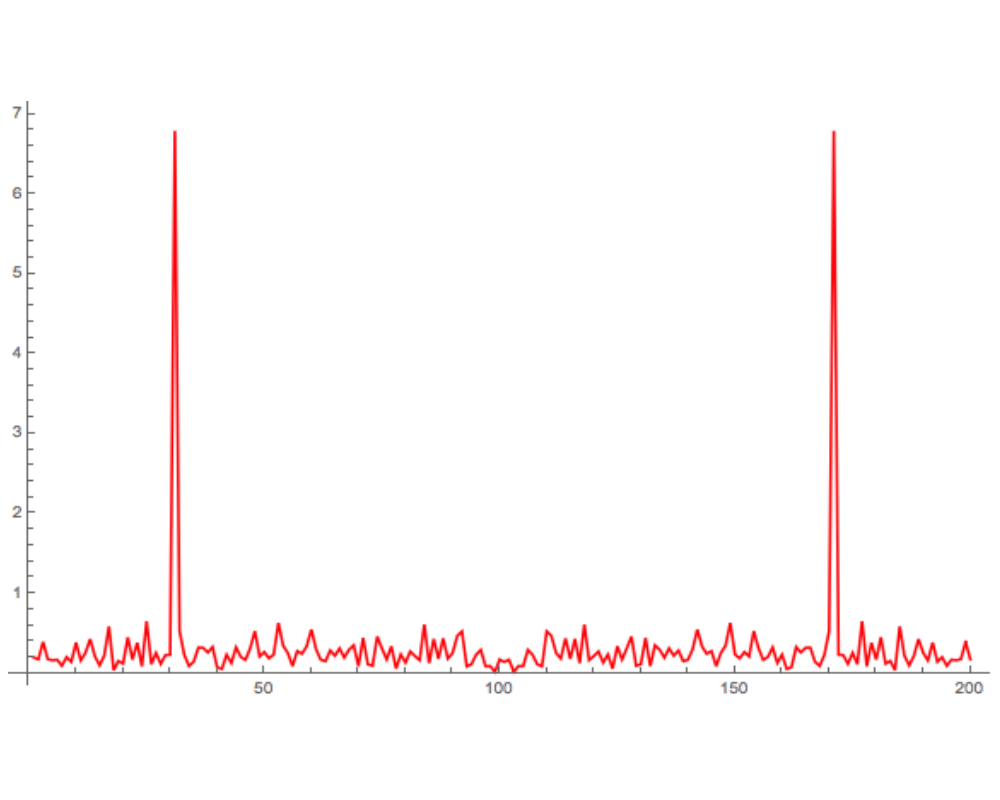
• Filtering: -- Taking the Fourier transform of a function is equivalent to representing it as the sum of sine functions. By eliminating undesirable high- and/or low-frequency components (i.e. dropping some of the sine functions) and taking an inverse Fourier transform to get us back into the time domain, we can filter an image to remove noise and other artifacts. For example, the sharp spike in the figure above describes the period of a single sine function that closely models the input data.

• Image Compression -- A smoothed, filtered image contains less information than a noisy image, while retaining a similar appearance. Thus encoding the smoothed image will require fewer bits to represent than the original image. By eliminating the coefficients of sine functions that contribute relatively little to the image, we can further reduce the size of the image, at little cost in image fidelity.

• Convolution and Deconvolution -- Fourier transforms can be used to efficiently compute convolutions of two sequences. A convolution is the pairwise product of elements from two different sequences, such as in multiplying two \(n\)-variable polynomials \(f\) and \(g\) or multiplying two long integers. Implementing the product directly takes \(O(n²)\), while \(O(n \lg n)\) suffices using the fast Fourier transform. Another example comes from image processing. \index{scanner, OCR} Because a scanner measures the darkness of an image patch instead of a single point, the scanned input is always blurred. A reconstruction of the original signal can be obtained by deconvoluting the input signal with a Gaussian point-spread function.

Implementations

FFTPACK (rating 10)	FFTW (rating 10)
fftw3 (rating 9)	GSL (rating 9)
FFT (rating 7)	Netlib (rating 5)
Moret and Shapiro's Algorithms P to NP (rating 3)

Recommended Books

Algorithms in Java, Third Edition (Parts 1-4) by Robert Sedgewick and Michael Schidlowsky	A Primer on Wavelets and Their Scientific Applications by J. Walker	The Fourier Transform and its Applications by R. Bracewell
Numerical Recipes in C by William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery	The Fast Fourier Transform and Its Applications by E. Oran Brigham

Related Problems

Arbitrary-Precision Arithmetic

Simplifying Polygons

Text Compression

As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.