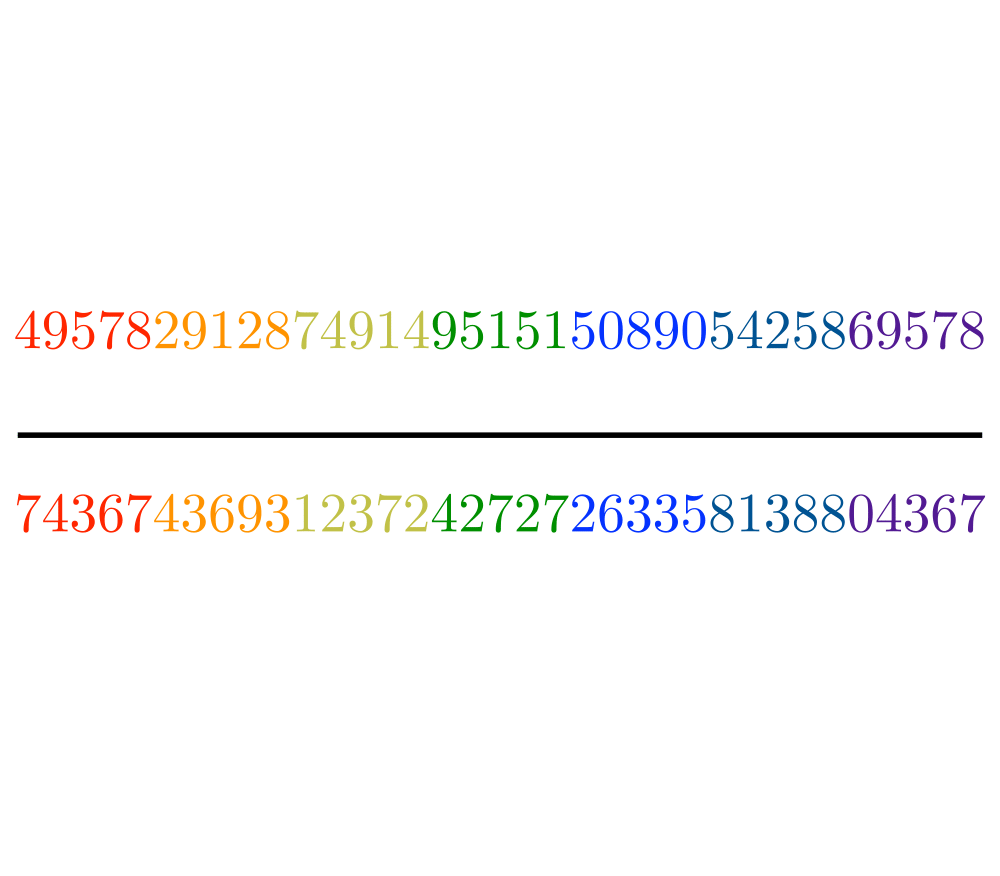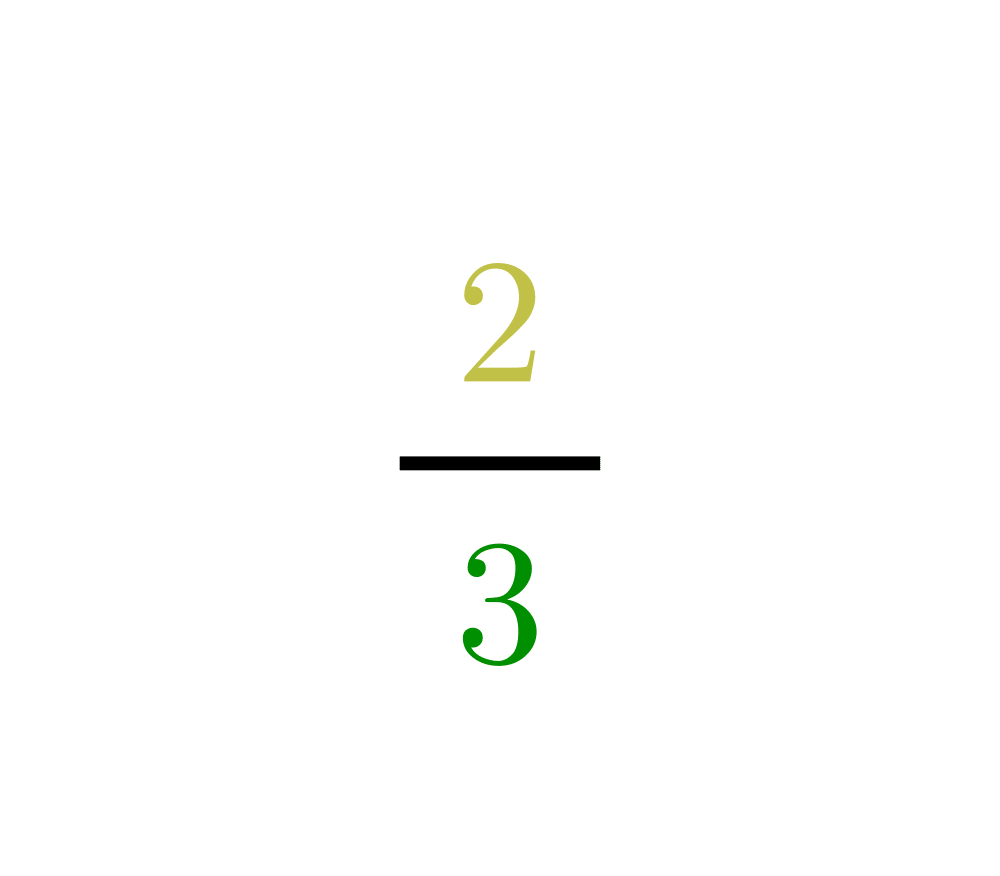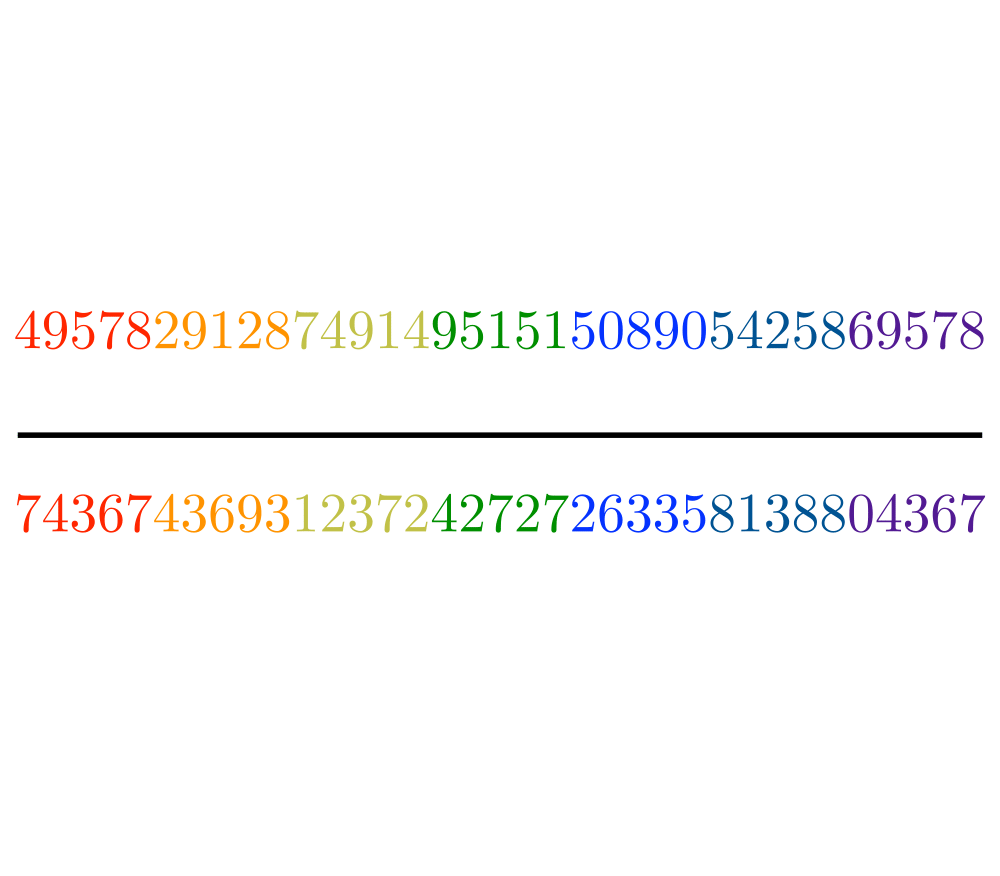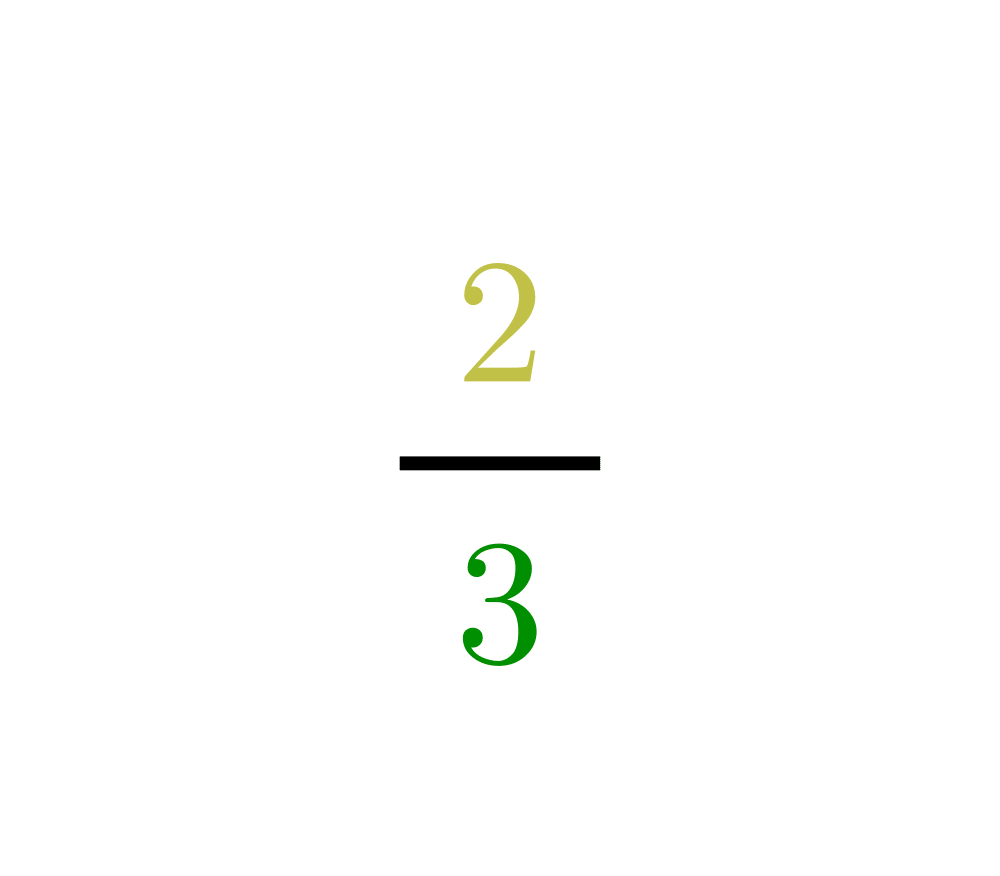 |
 |
|
|
Input Description: Two very large integers, \(x\) and \(y\).
Problem: What is \(x+y\), \(x-y\), \(x x y\) and \(x / y\)?
Excerpt from The Algorithm Design Manual: Any programming language whose level rises above basic assembler supports single- and perhaps double-precision integer/real addition, subtraction, multiplication, and division. But what if we wanted to represent the national debt of the United States in pennies? One trillion dollars worth of pennies requires 15 decimal digits, which is far more than can fit into a 32-bit integer.
In other applications much larger integers are needed. The RSA algorithm for public-key cryptography requires integer keys of at least 100 digits to achieve any level of security, and 1000 digits are recommended. Experimenting with number-theoretic conjectures for fun or research always requires playing with large numbers.
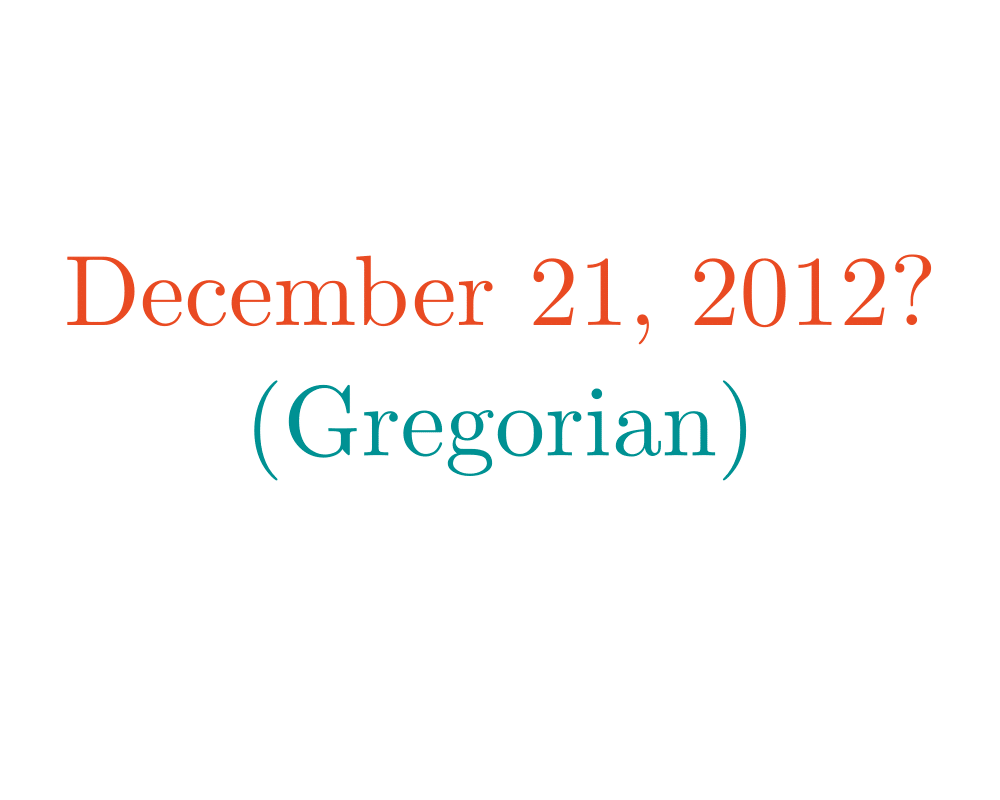  Calendrical Calculations |
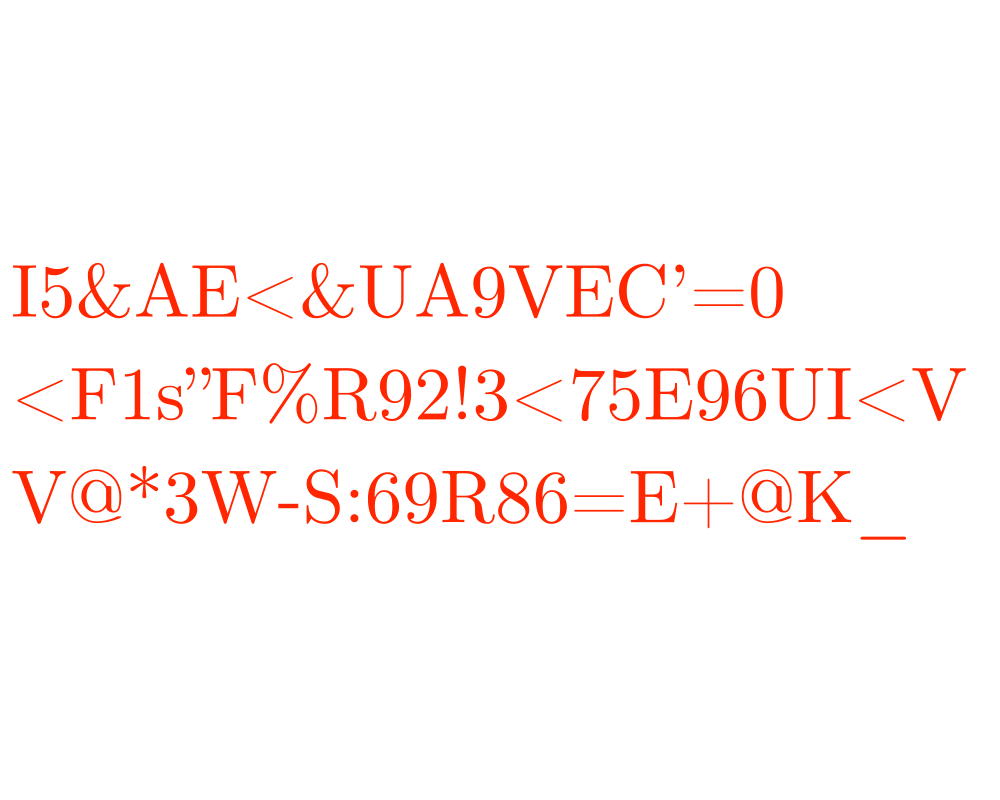  Cryptography |
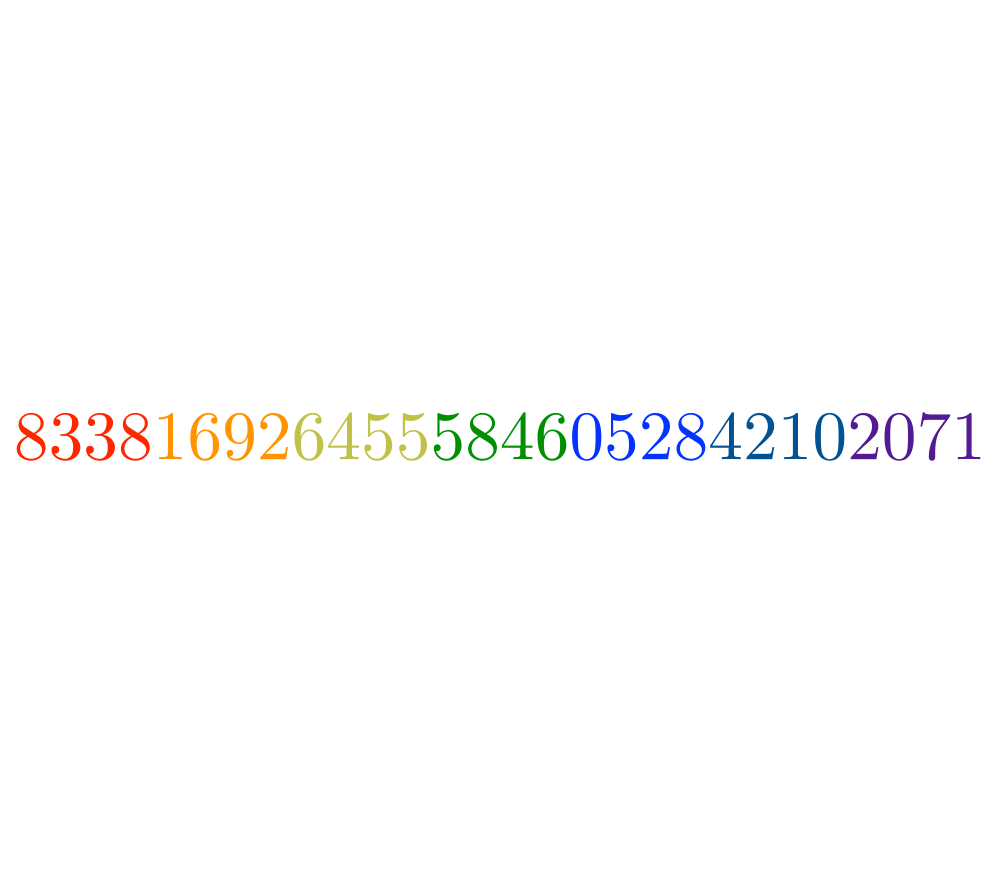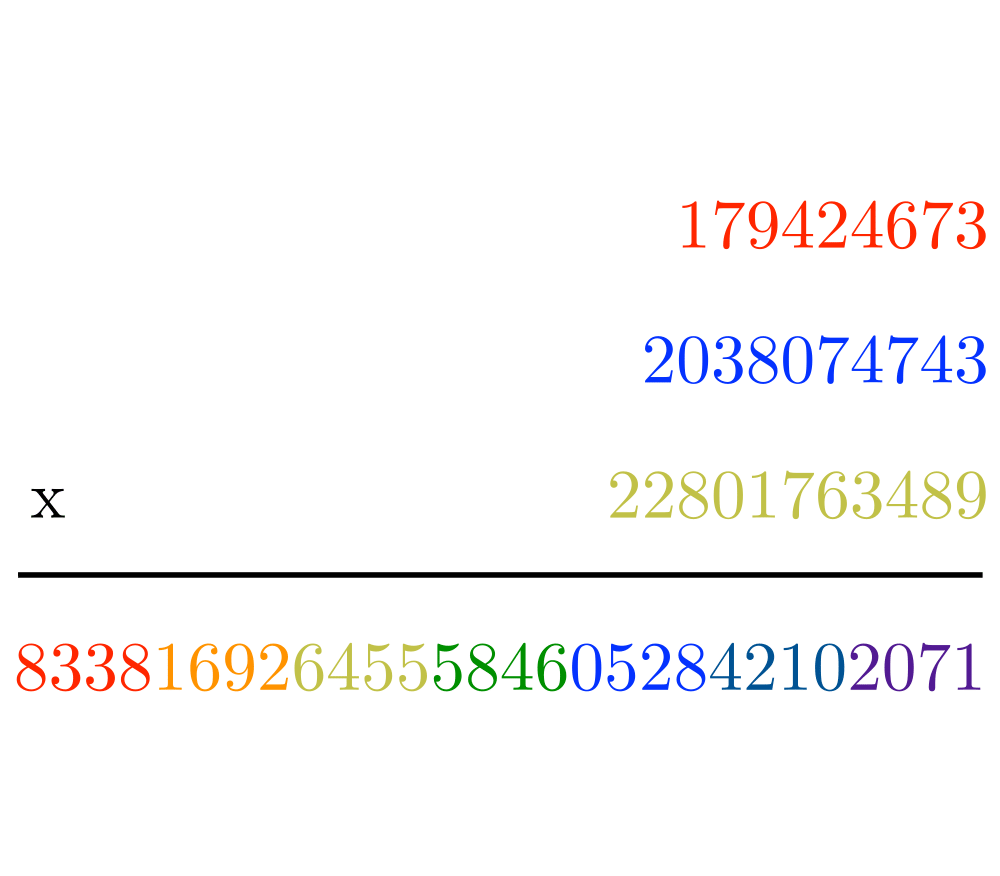  Factoring and Primality Testing |
  Discrete Fourier Transform |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
A Computational Introduction to Number Theory and Algebra by V. Shoup.jpg)
Algorithms in Java, Third Edition (Parts 1-4) by Robert Sedgewick and Michael Schidlowsky
The Art of Computer Programming : Seminumerical Algorithms by Donald Knuth
Algorithmic Number Theory : Efficient Algorithms by Eric Bach and Jeffrey Shallit
Introduction to Algorithms by T. Cormen and C. Leiserson and R. Rivest and C. Stein
The Design and Analysis of Computer Algorithms by A. Aho and J. Hopcroft and J. Ullman