 |
 |
|
|
Input Description: An integer \(n\).
Problem: Generate (1) all, or (2) a random, or (3) the next permutation of length \(n\).
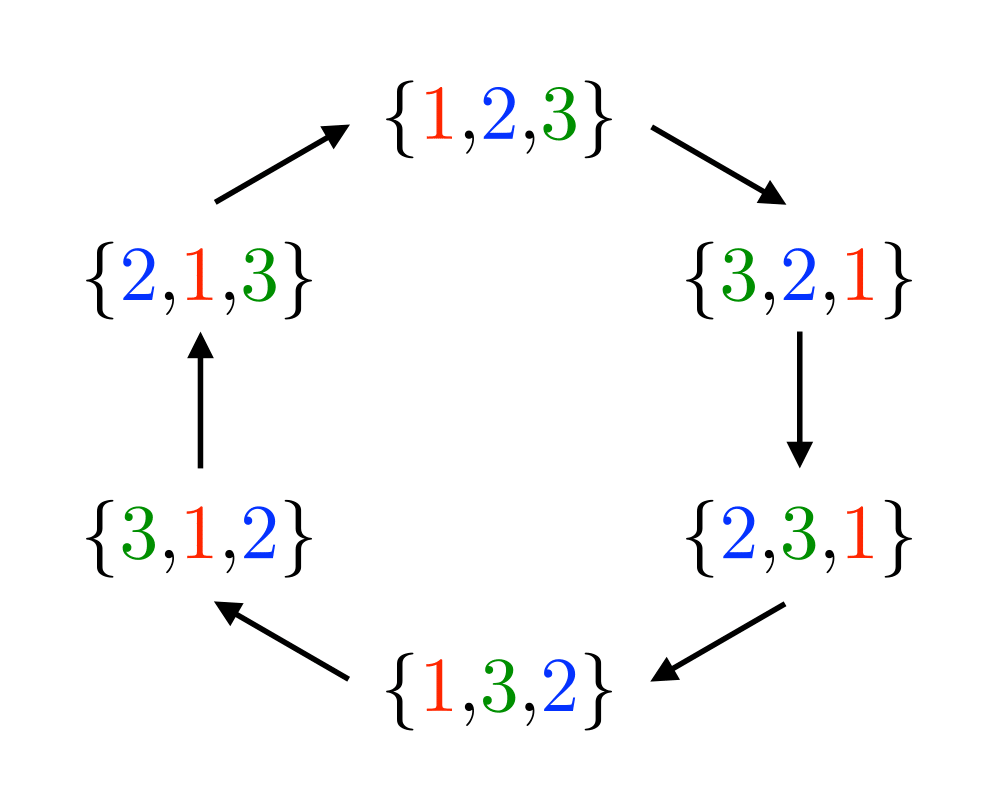
Excerpt from The Algorithm Design Manual: Fundamental to any permutation-generation algorithm is a notion of order, the sequence in which the permutations are constructed, from first to last. The most natural generation order is lexicographic, the order they would appear if they were sorted numerically. Lexicographic order for \(n=3\) is \(\{1,2,3\}\), \(\{1,3,2\}\), \(\{2,1,3\}\), \(\{2,3,1\}\), \(\{3,1,2\}\), and finally \(\{3,2,1\}\). Although lexicographic order is aesthetically pleasing, there is often no particular reason to use it. For example, if you are searching through a collection of files, it does not matter whether the filenames are encountered in sorted order, so long as you search through all of them. Indeed, nonlexicographic orders lead to faster and simpler permutation generation algorithms.
There are two different paradigms for constructing permutations: ranking/unranking and incremental change methods. Although the latter are more efficient, ranking and unranking can be applied to solve a much wider class of problems, including the other combinatorial generation problems.
 The Art of Computer Programming, Volume 4 Fascicle 2: Generating All Tuples and Permutations by D. E. Knuth |
 Tables of Random Permutations by L. E. Moses and R. V. Oakford |
  Calendrical Calculations |
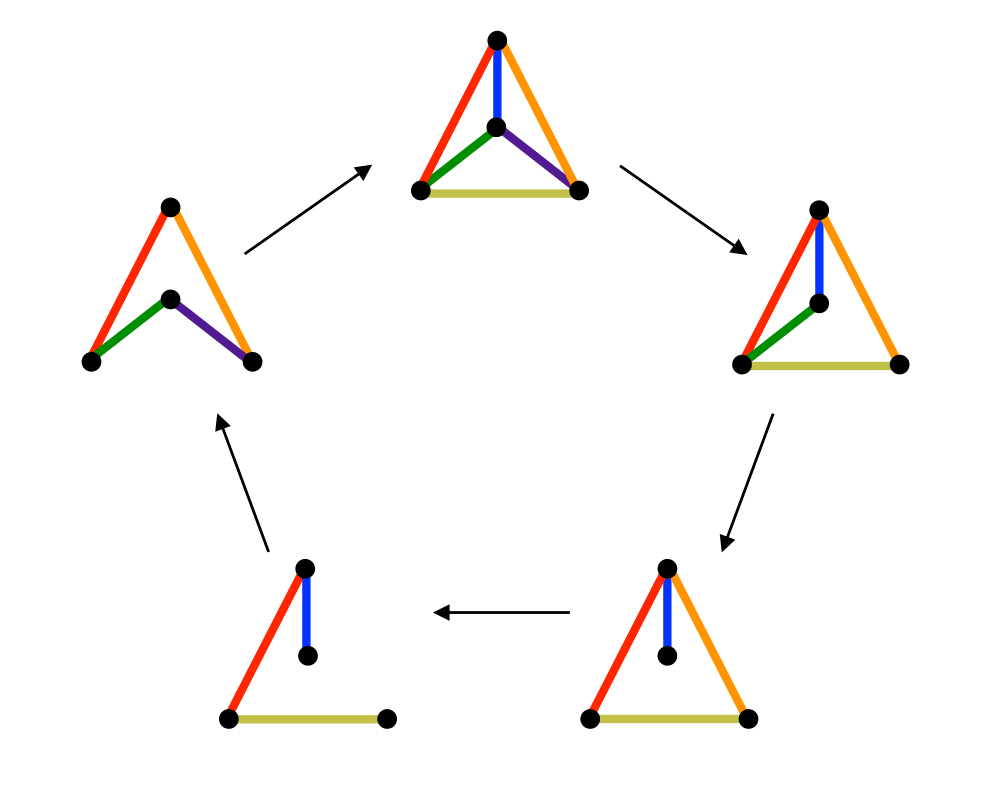  Generating Graphs |
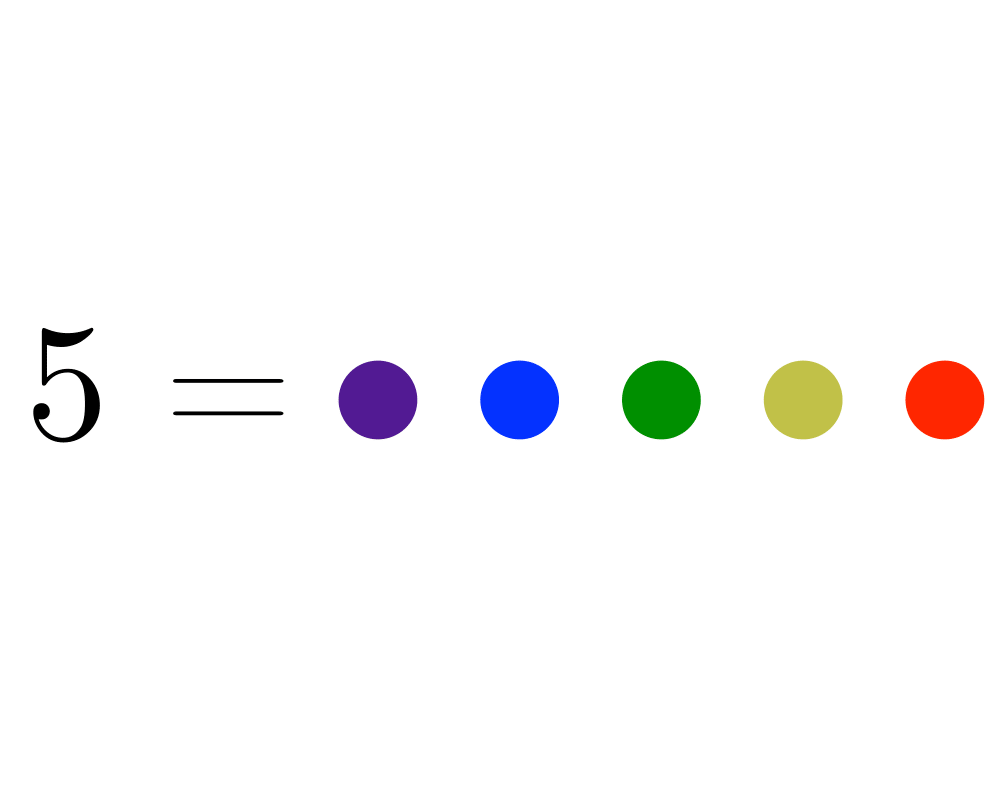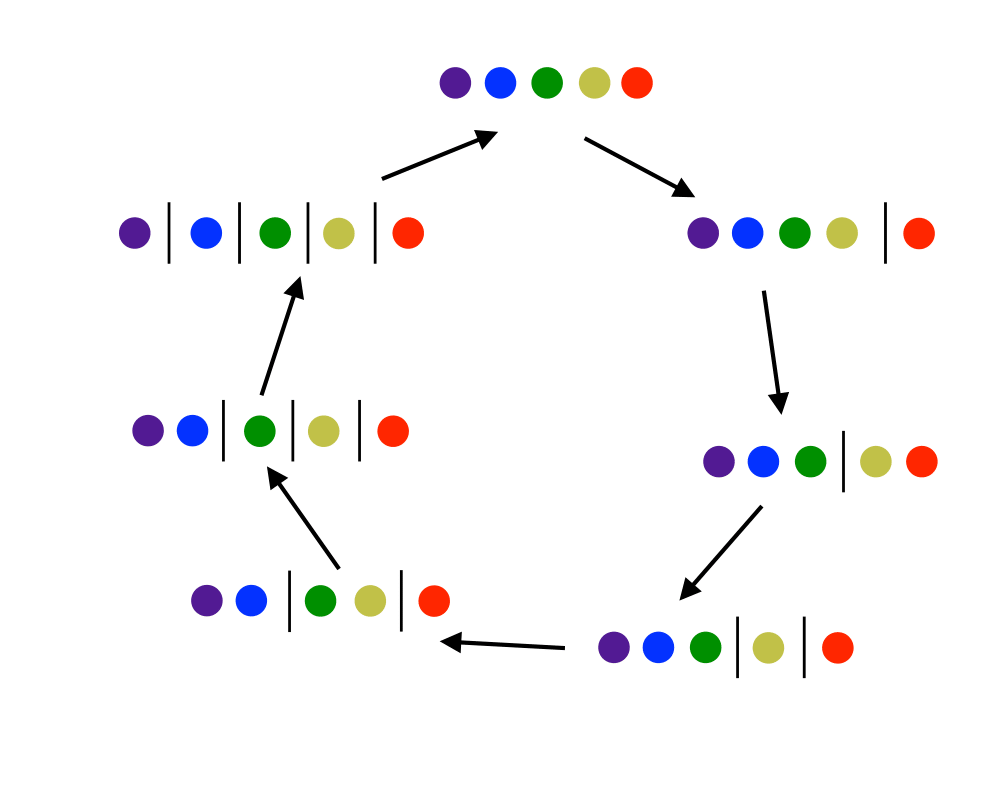  Generating Partitions |
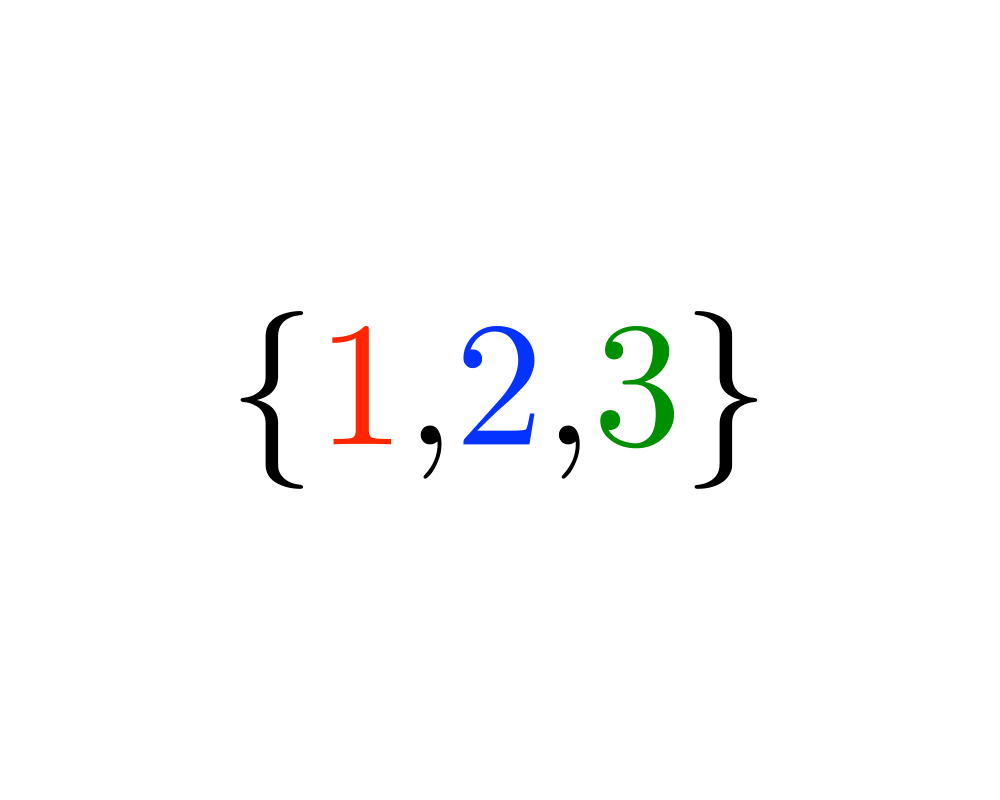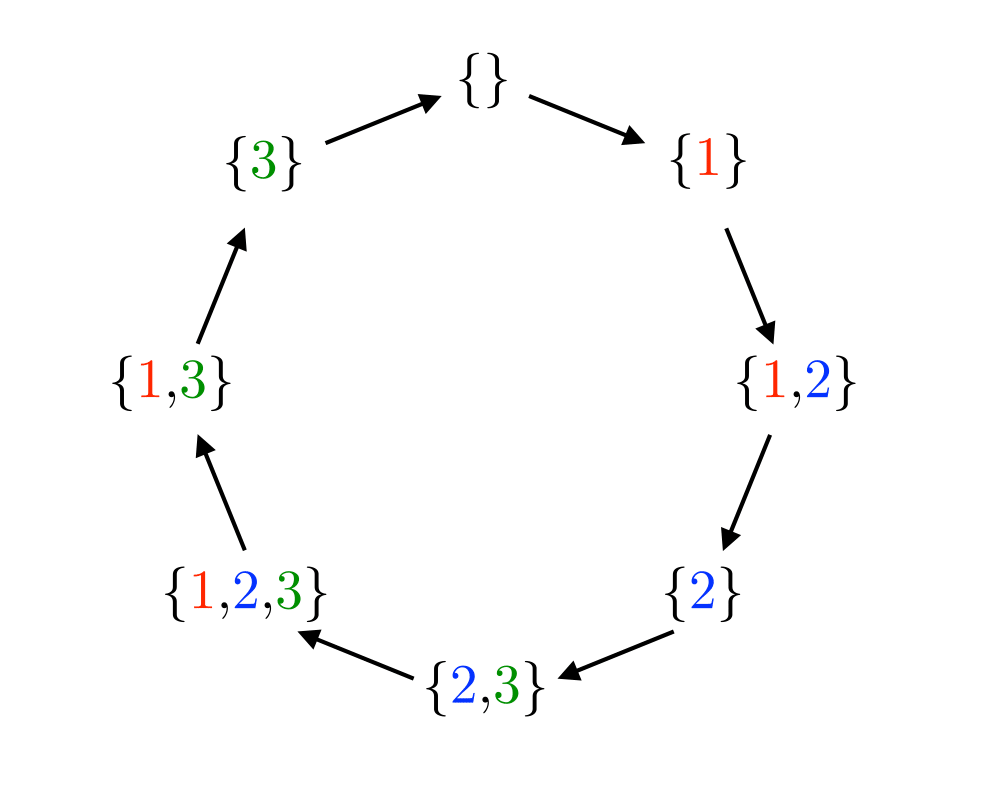  Generating Subsets |
  Random Number Generation |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.