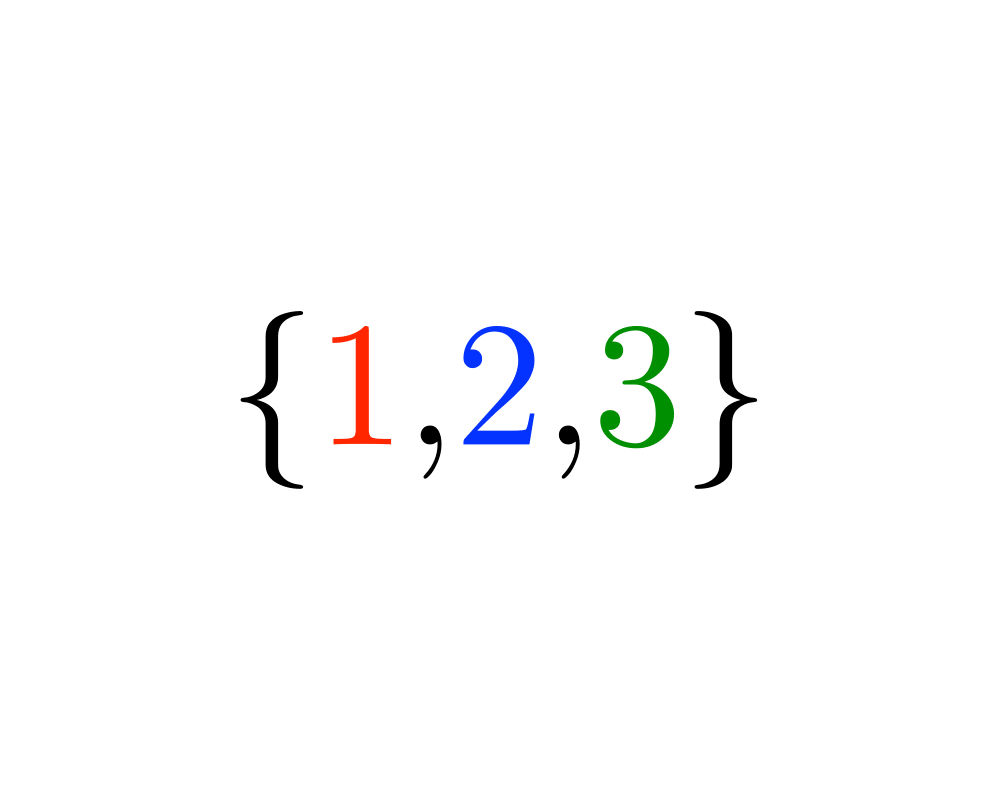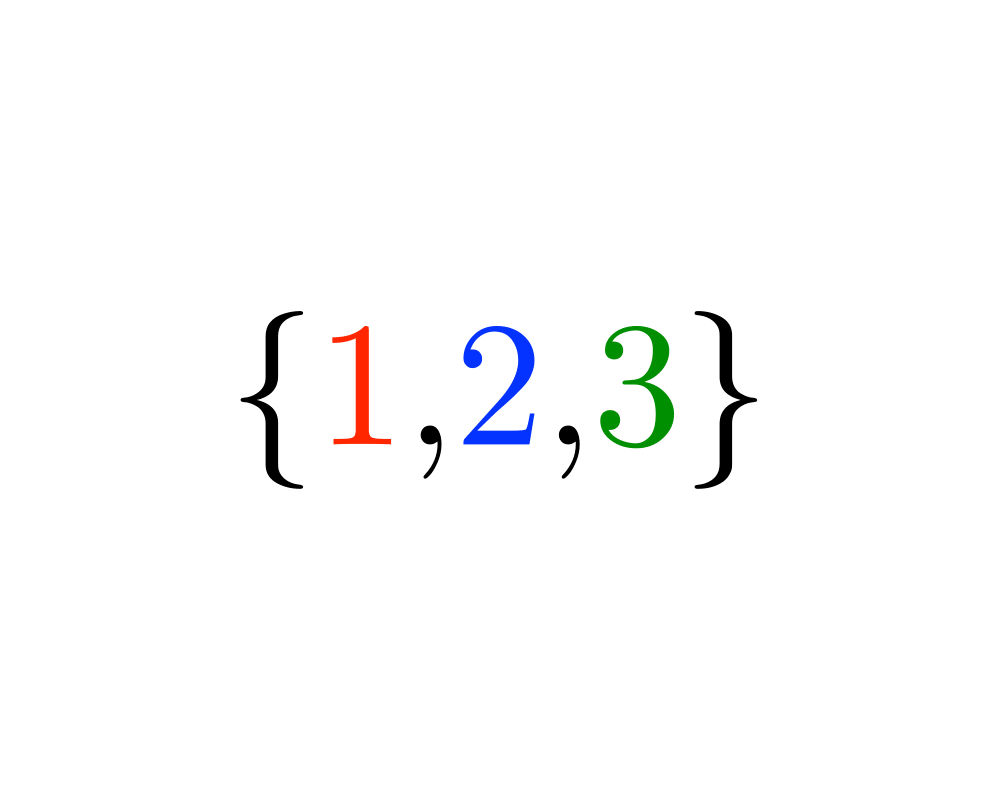 |
 |
|
|
Input Description: An integer \(n\).
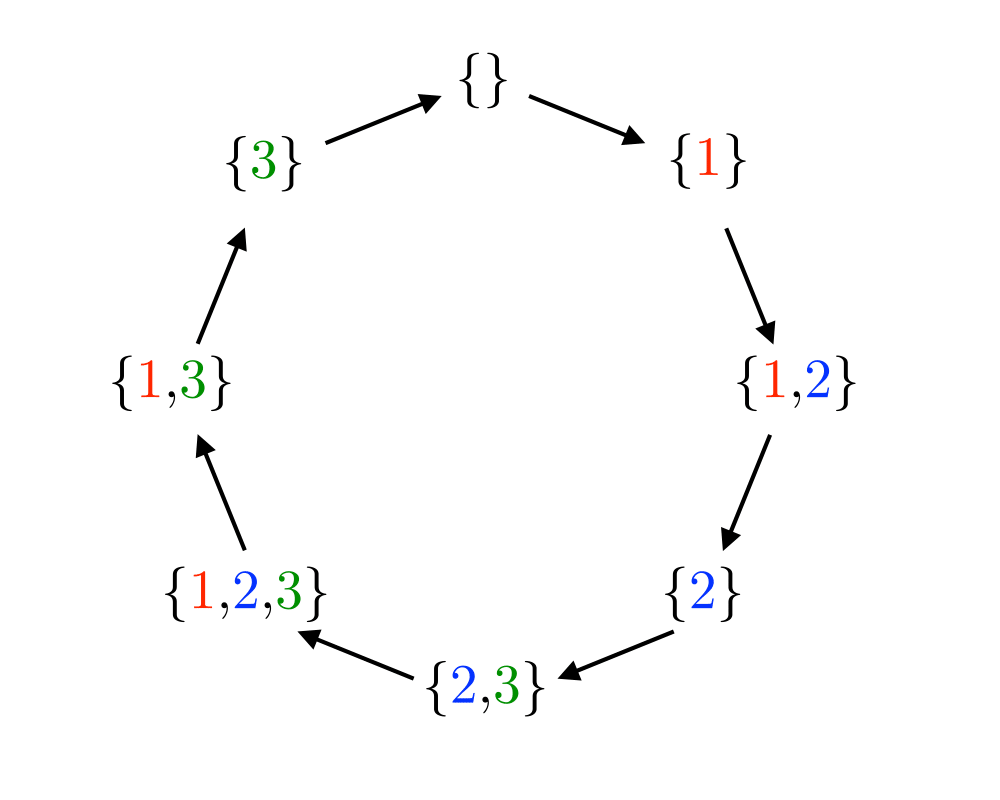
Problem: Generate (1) all, or (2) a random, or (3) the next subset of the integers \(1\) to \(n\).
Excerpt from The Algorithm Design Manual: A subset describes a selection of objects, where the order among them does not matter. Many of the algorithmic problems in this catalog seek the best subset of a group of things: vertex cover seeks the smallest subset of vertices to touch each edge in a graph; knapsack seeks the most profitable subset of items of bounded total size; and set packing seeks the smallest subset of subsets that together cover each item exactly once.
There are \(2n\) distinct subsets of an \(n\)-element set, including the empty set as well as the set itself. This grows exponentially, but at a considerably smaller rate than the \(n!\) permutations of \(n\) items. Indeed, since \(220 =\) 1,048,576, a brute-force search through all subsets of 20 elements is easily manageable, although by \(n=30\), \(230 =\) 1,073,741,824, so you will certainly be pushing things.
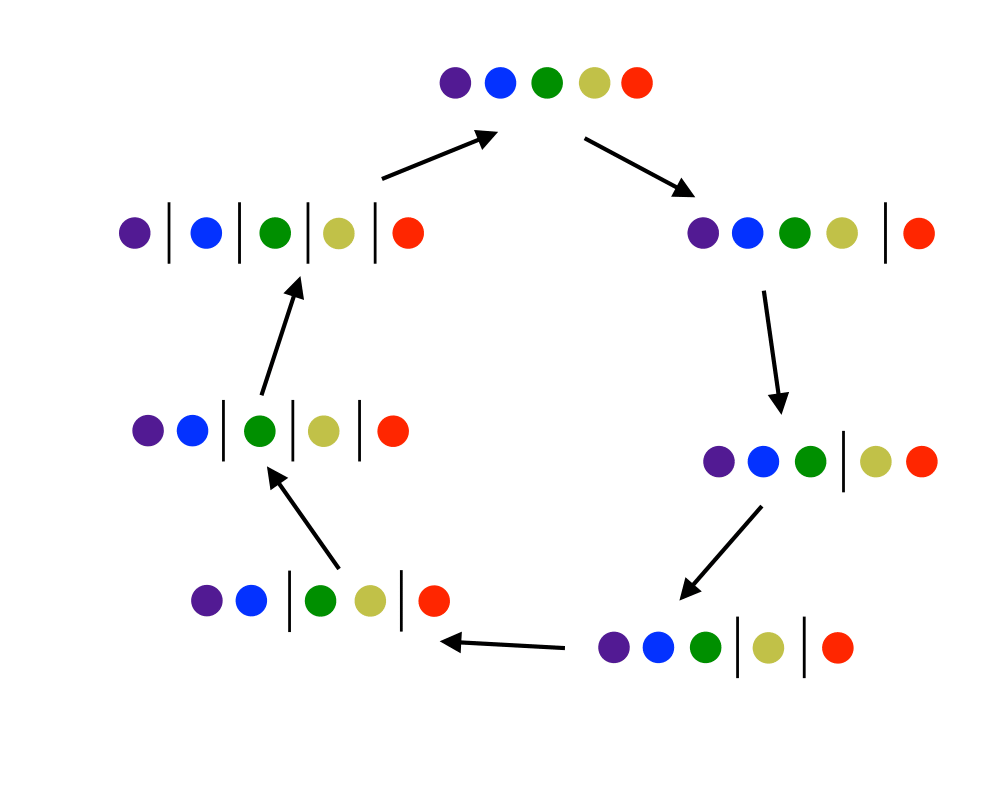  Generating Partitions |
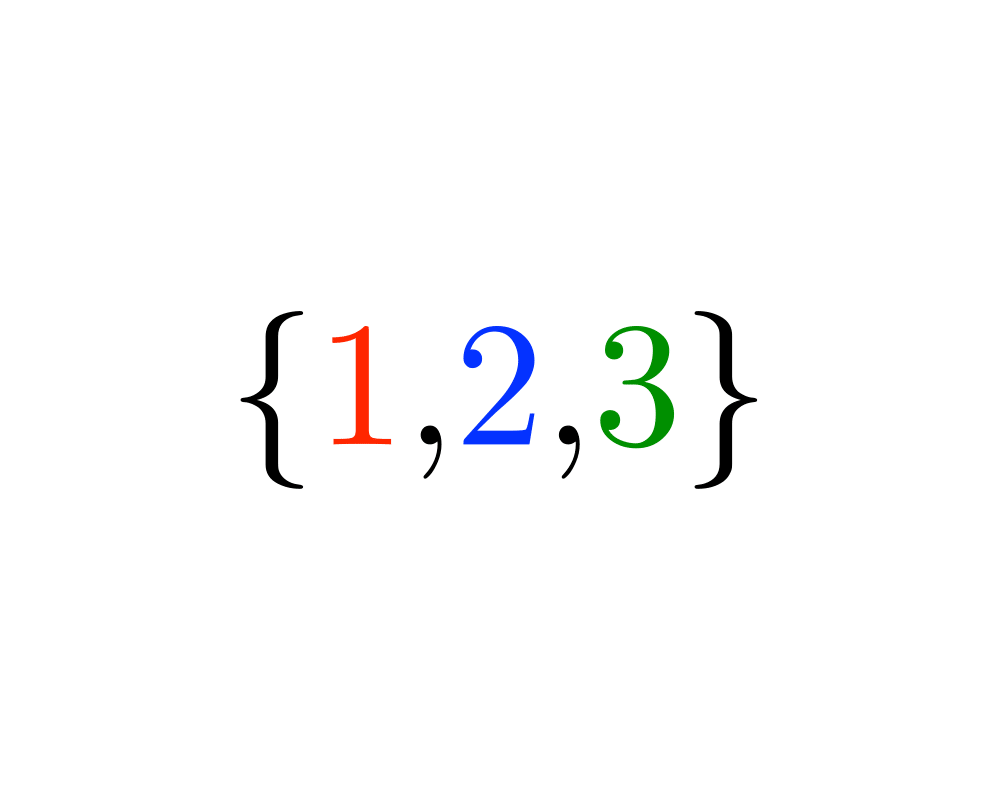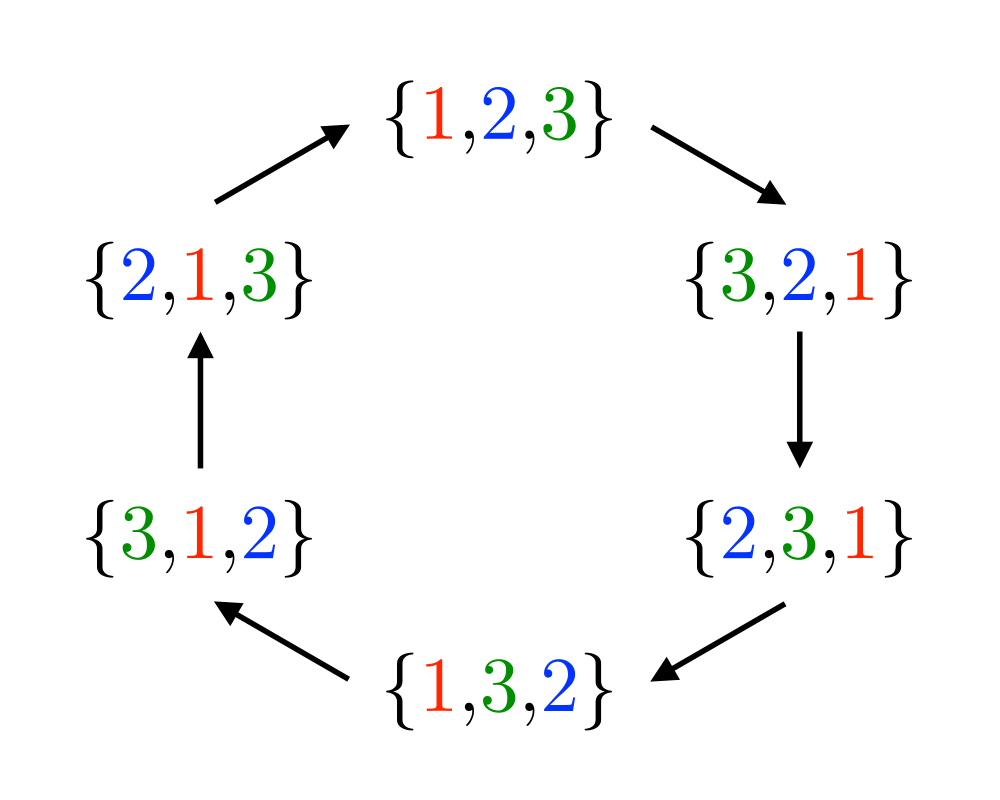  Generating Permutations |
  Random Number Generation |
  Set Data Structures |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
The Art of Computer Programming, Volume 4 Fascicle 3: Generating All Combinations and Partitions by D. E. Knuth
Combinatorial Algorithms : Generation, Enumeration, and Search by Donald L. Kreher and Douglas R. Stinson
Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica by S. Pemmaraju and S. Skiena
Combinatorial Algorithms: an update by H. Wilf
Combinatorial Algorithms for Computers and Calculators by A. Nijenhuis and H. Wilf