 |
 |
 |
 |
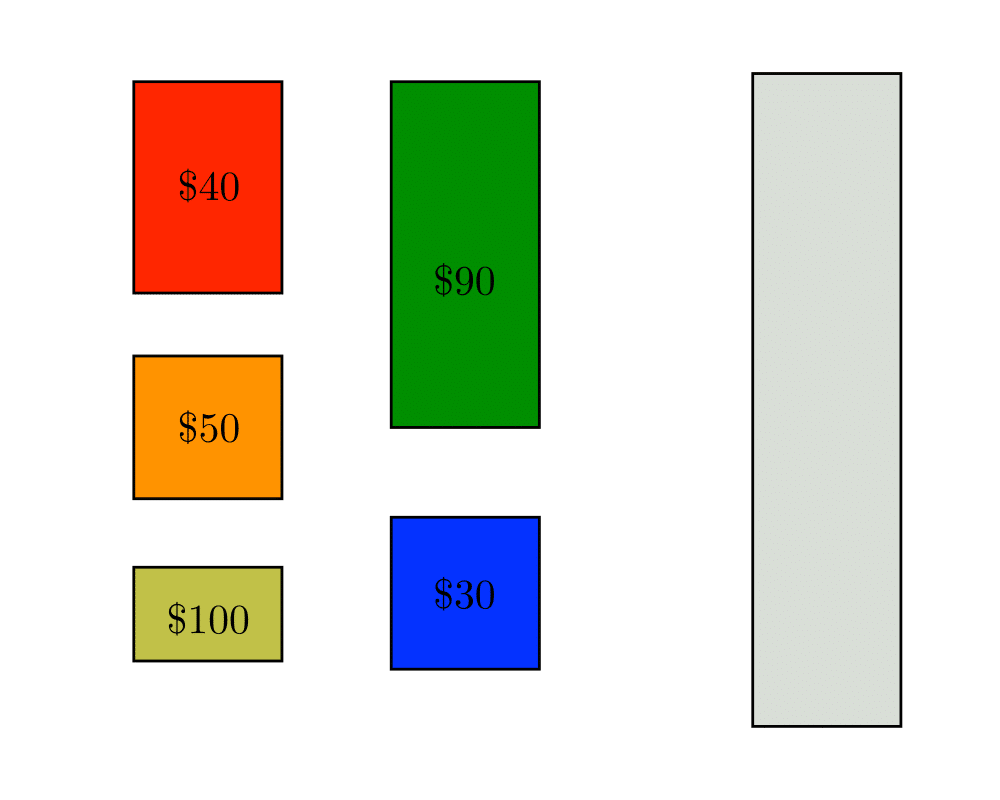
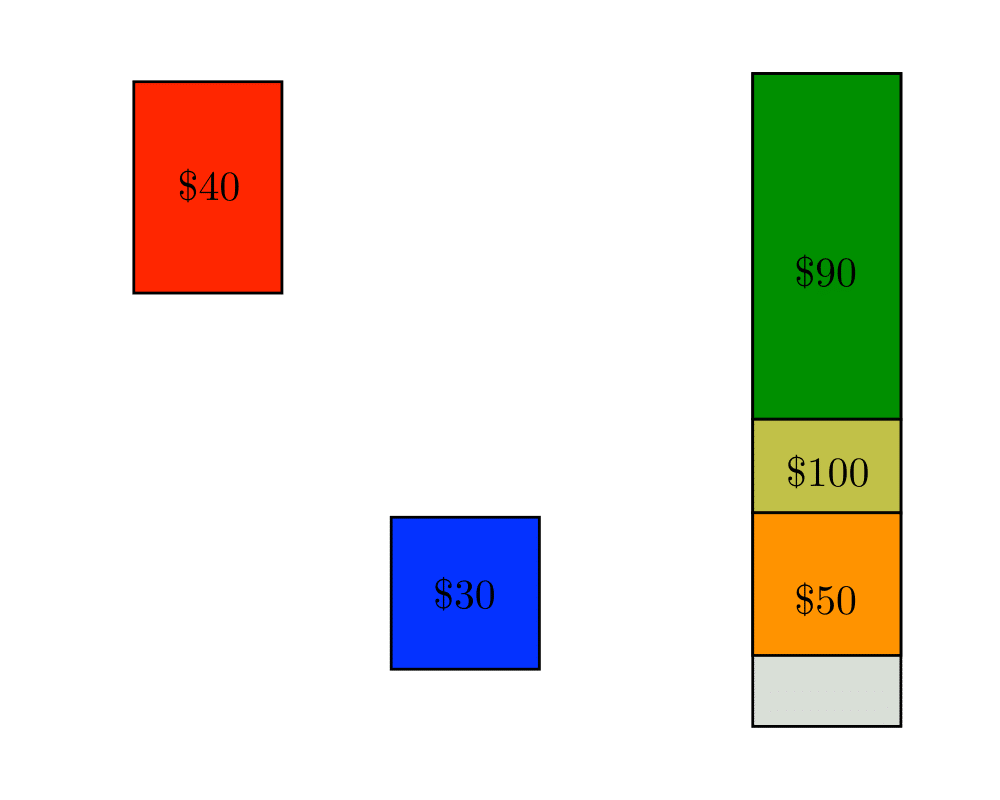
Input Description: A set of items \(S=\{1,...,n\}\), where item \(i\) has size \(s_i\) and value \(v_i\). A knapsack capacity \(C\).
Problem: Find the subset \(S' \subset S\) which maximizes the value of \(\sum_{i \in S'} v_i\) given that \(\sum_{i \in S'} s_i \leq C\), ie. fits in a knapsack of size \(C\).
Excerpt from The Algorithm Design Manual: The knapsack problem arises whenever there is resource allocation with financial constraints. Given a fixed budget, how do you select what things you should buy. Everything has a cost and value, so we seek the most value for a given cost. The term knapsack problem invokes the image of the backbacker who is constrained by a fixed-size knapsack and so must fill it only with the most useful items.
The typical formulation in practice is the 0/1 knapsack problem, where each item must be put entirely in the knapsack or not included at all. Objects cannot be broken up arbitrarily, so its not fair taking one can of coke from a six-pack or opening the can to take just a sip. It is this \(0/1\) property that makes the knapsack problem hard, for a simple greedy algorithm finds the optimal selection whenever we are allowed to subdivide objects arbitrarily. For each item, we could compute its ``price per pound'', and take as much of the most expensive item until we have it all or the knapsack is full. Repeat with the next most expensive item, until the knapsack is full. Unfortunately, this \(0/1\) constraint is usually inherent in most applications.
| Silvano Martello and Paolo Toth's Knapsack Problem (rating 10) |
David Pisinger's optimization codes (rating 9) |
| BoxPacker (rating 8) |
Netlib (rating 5) |
| Discrete Optimization Methods (rating 3) |
  Bin Packing |
  Linear Programming |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.