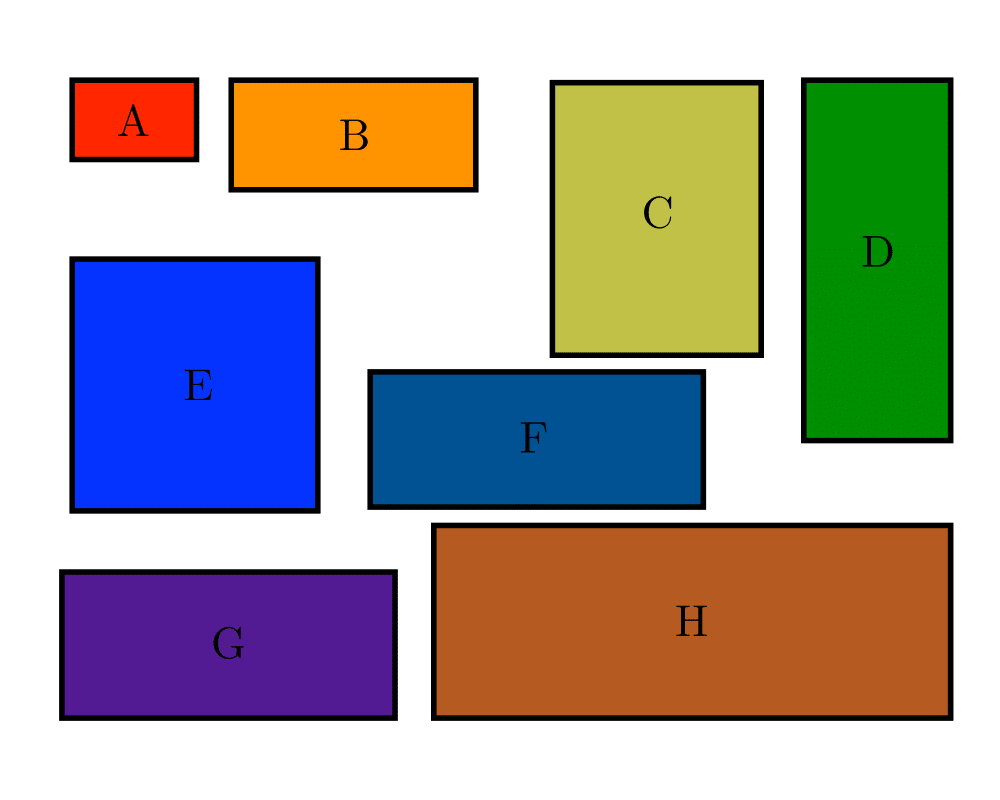
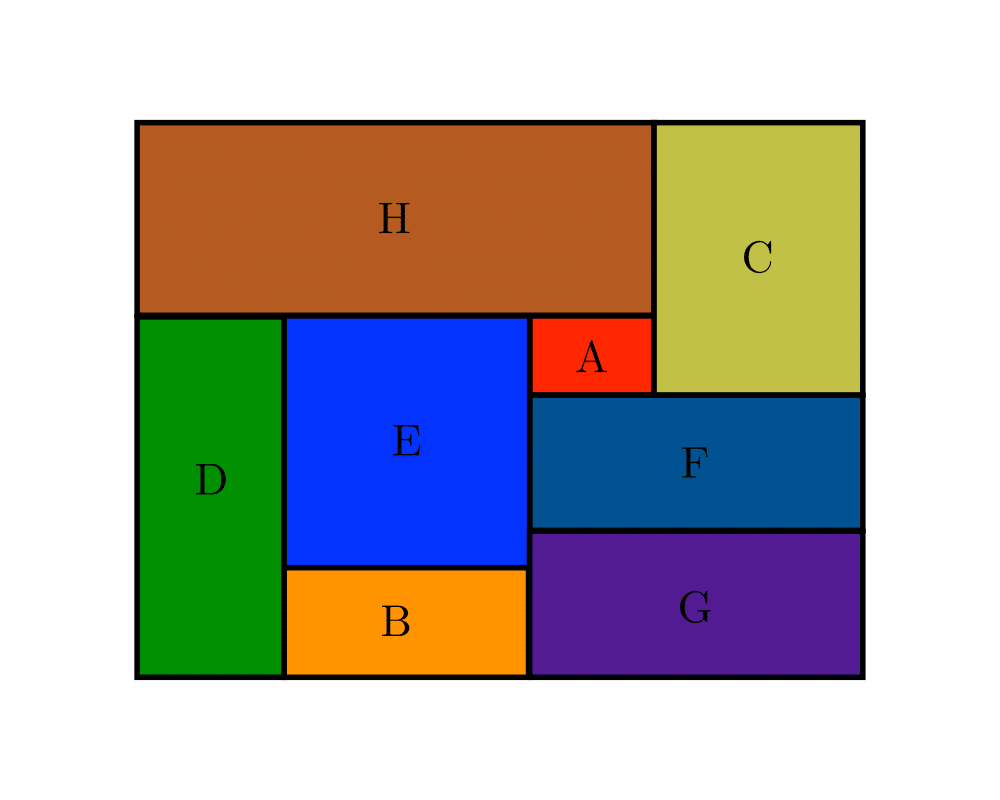
 |
 |
|
|
Input Description: A set of \(n\) items with sizes \(d_1,...,d_n\). A set of \(m\) bins with capacity \(c_1,...,c_m\).
Problem: How do you store the set of items using the fewest number of bins?
Excerpt from The Algorithm Design Manual: Bin packing arises in a variety of packaging and manufacturing problems. Suppose that you are manufacturing widgets with parts cut from sheet metal, or pants with parts cut from cloth. To minimize cost and waste, we seek to lay out the parts so as to use as few fixed-size metal sheets or bolts of cloth as possible. Identifying which part goes on which sheet in which location is a bin-packing variant called the cutting stock problem. After our widgets have been successfully manufactured, we will be faced with another bin packing problem, namely how best to fit the boxes into trucks to minimize the number of trucks needed to ship everything.
| Silvano Martello and Paolo Toth's Knapsack Problem (rating 9) |
David Pisinger's optimization codes (rating 8) |
| RectangleBinPack (rating 7) |
Program (rating 7) |
| BoxPacker (rating 6) |
bin-packing (rating 5) |
 Sphere packings, lattices, and groups by J. Conway and N. Sloane |
 Knapsack Problems : Algorithms and Computer Implementations by Silvano Martello and Paolo Toth |
 Computer Algorithms by S. Baase |
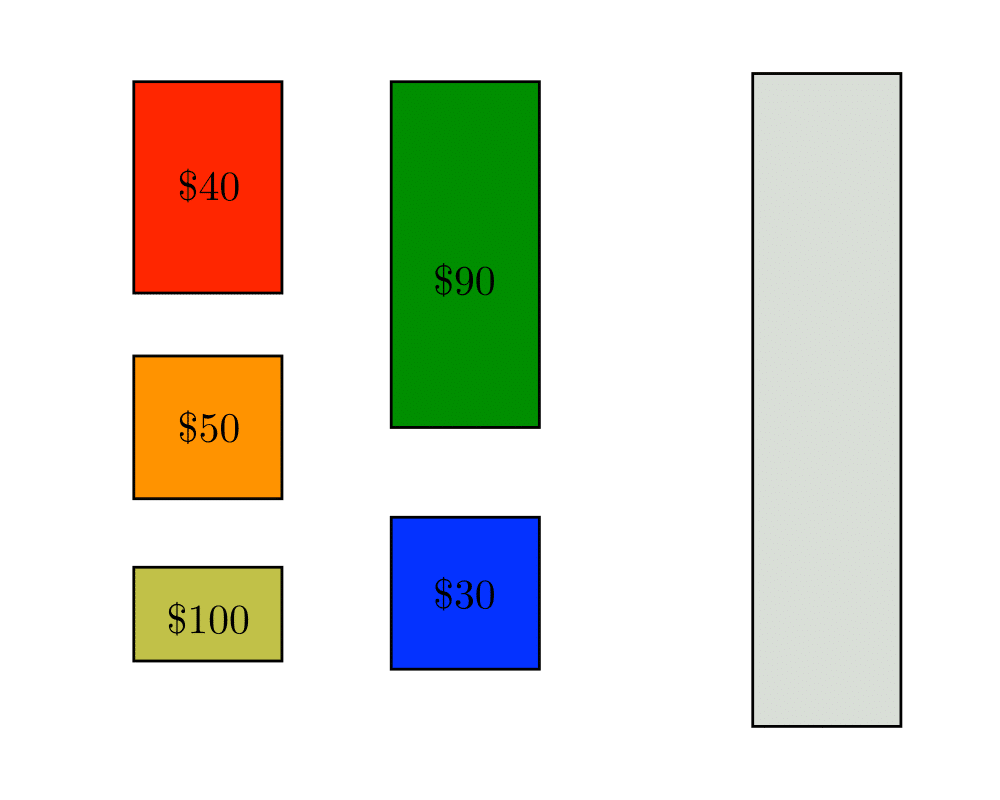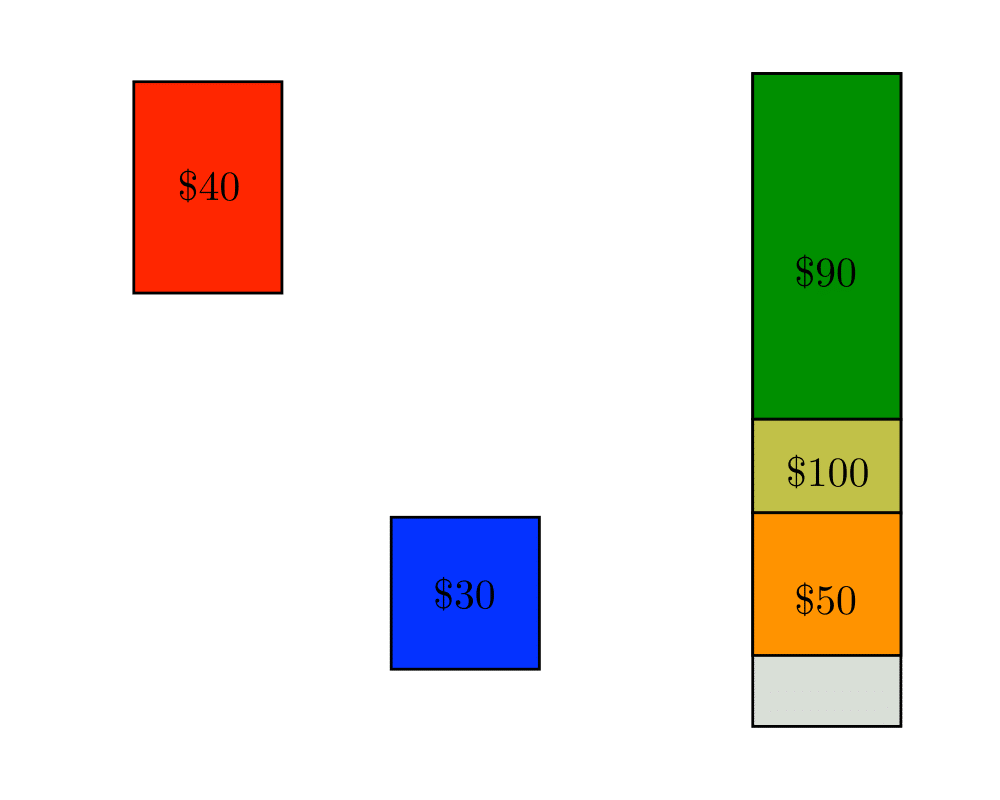  Knapsack Problem |
  Job Scheduling |
  Set Packing |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.