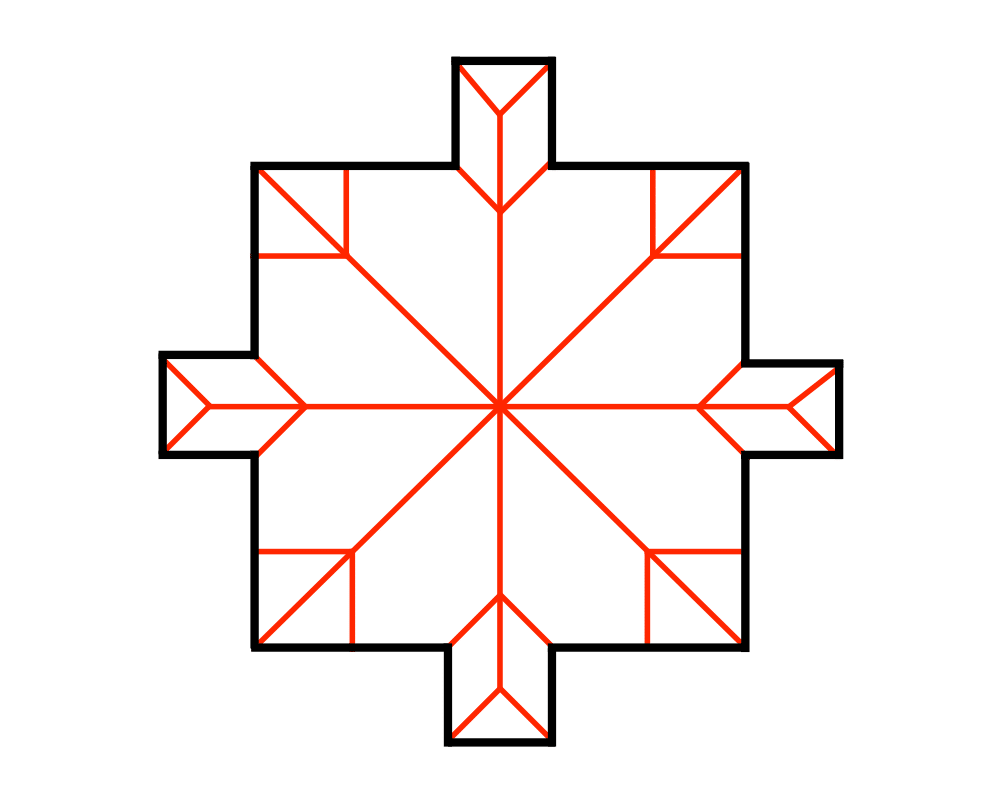
 |
 |
|
|
Input Description: A polygon or polyhedron \(P\).
Problem: What is the set of points within \(P\) which have more than one closest point on the boundary of \(P\)?
Excerpt from The Algorithm Design Manual: The medial-axis transformation is useful in thinning a polygon, or, as is sometimes said, finding its skeleton. The goal is to extract a simple, robust representation of the shape of the polygon. As can be seen from the figures above, the thinned versions of the letters capture the essence of the shape of an `A' and a `B', and would be relatively unaffected by changing the thickness of strokes or by adding font-dependent flourishes such as serifs.
The medial-axis transformation of a polygon is always a tree, making it fairly easy to use dynamic programming to measure the ``edit distance'' between the skeleton of a known model and the skeleton of an unknown object. Whenever the two skeletons are close enough, we can classify the unknown object as an instance of our model. This technique has proven useful in computer vision and in optical character recognition. The skeleton of a polygon with holes (like the `A' and `B') is not a tree, but an embedded planar graph, but it remains easy to work with.
| VRONI (rating 8) |
Cocone (rating 7) |
| Power Crust (rating 7) |
Skeletonization Software (rating 5) |
| masbcpp (rating 4) |
MedialAxisTransform (rating 3) |
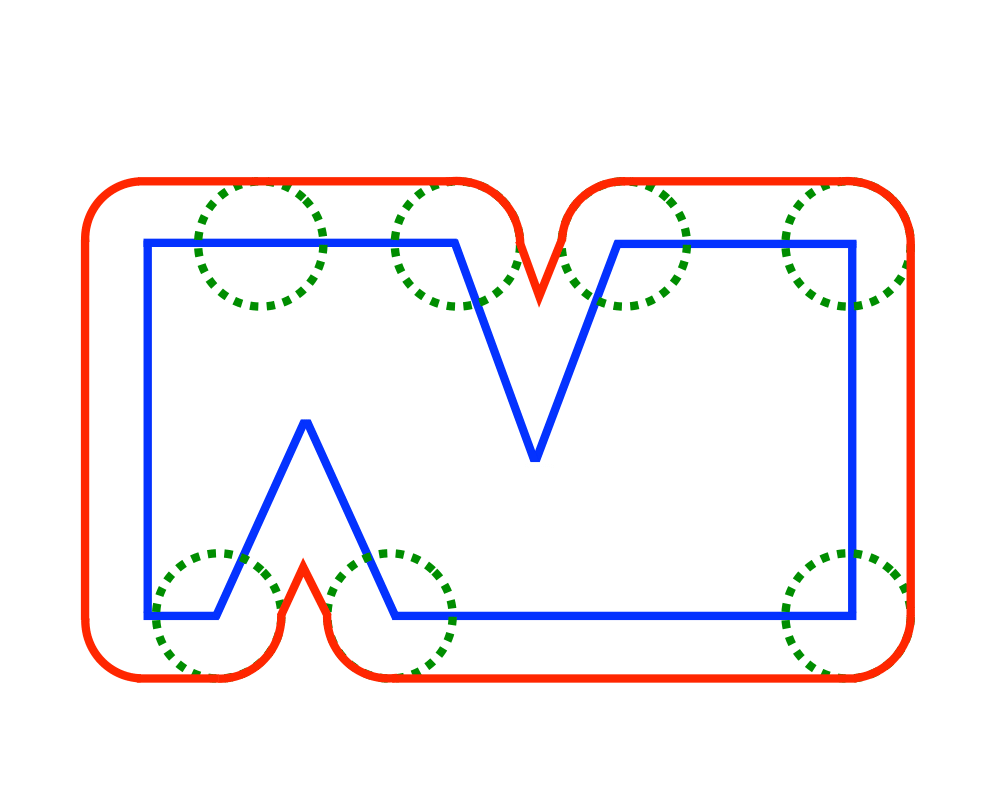  Minkowski Sum |
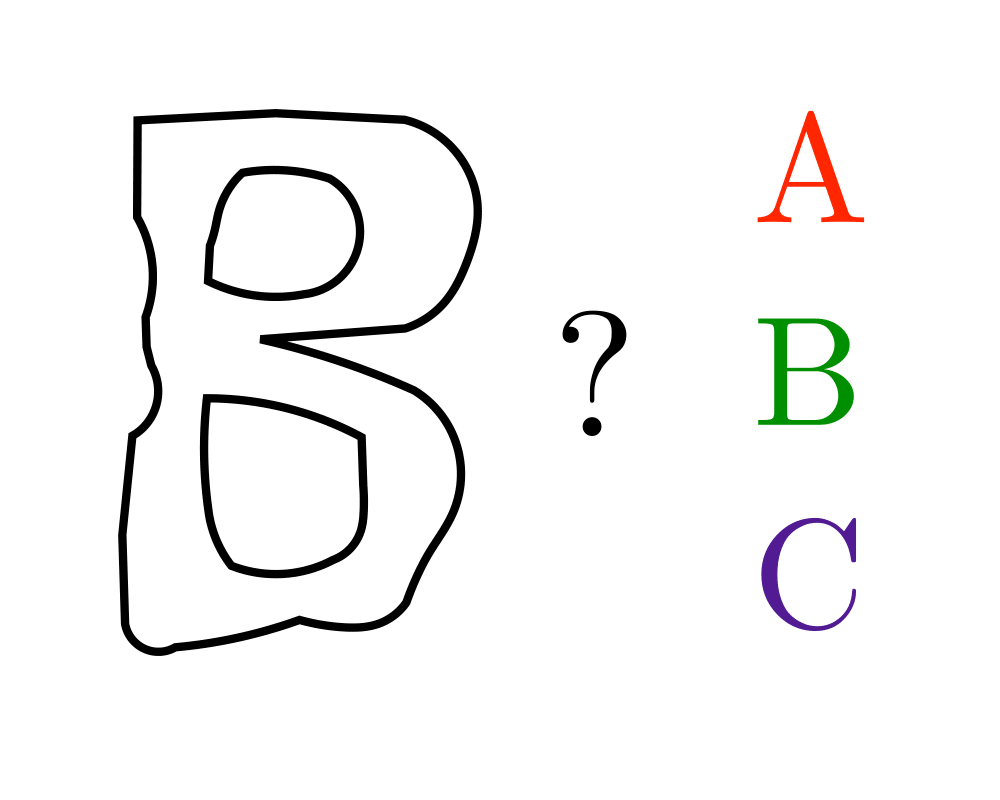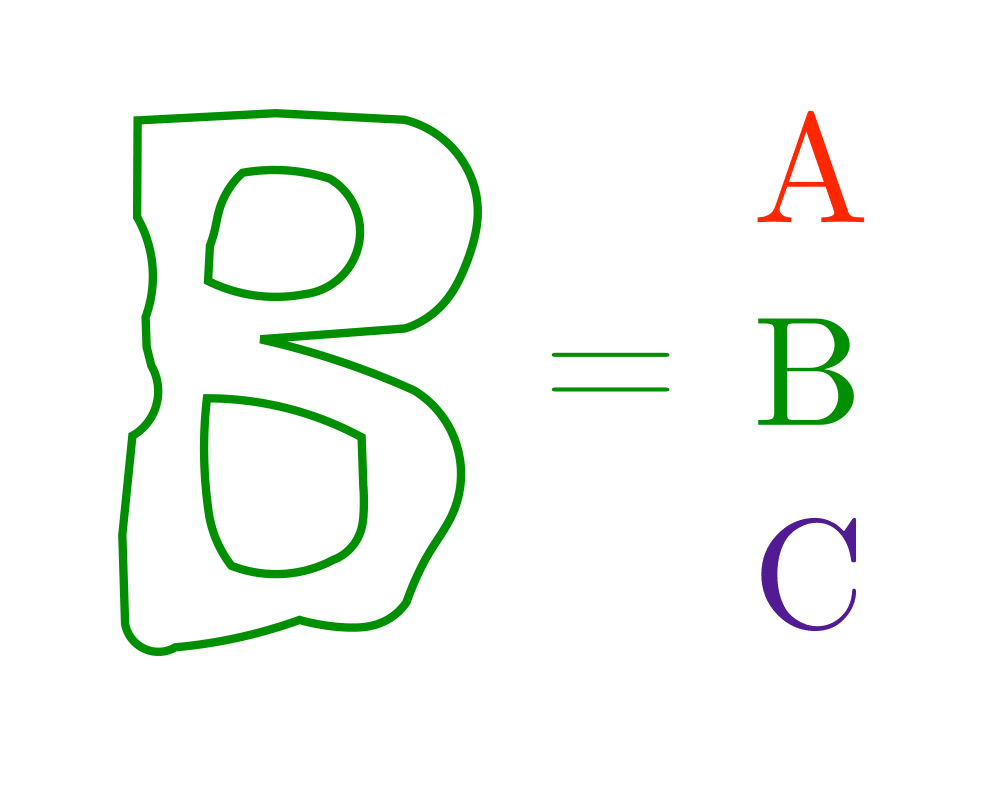  Shape Similarity |
  Voronoi Diagrams |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
Computational Geometry in C by Joseph O'Rourke
Discrete Voronoi Skeletons by R. Ogniewicz
Algorithms for Graphics and Image Processing by T. Pavlidis
Pattern Classification and Scene Analysis by R. Duda and P. Hart