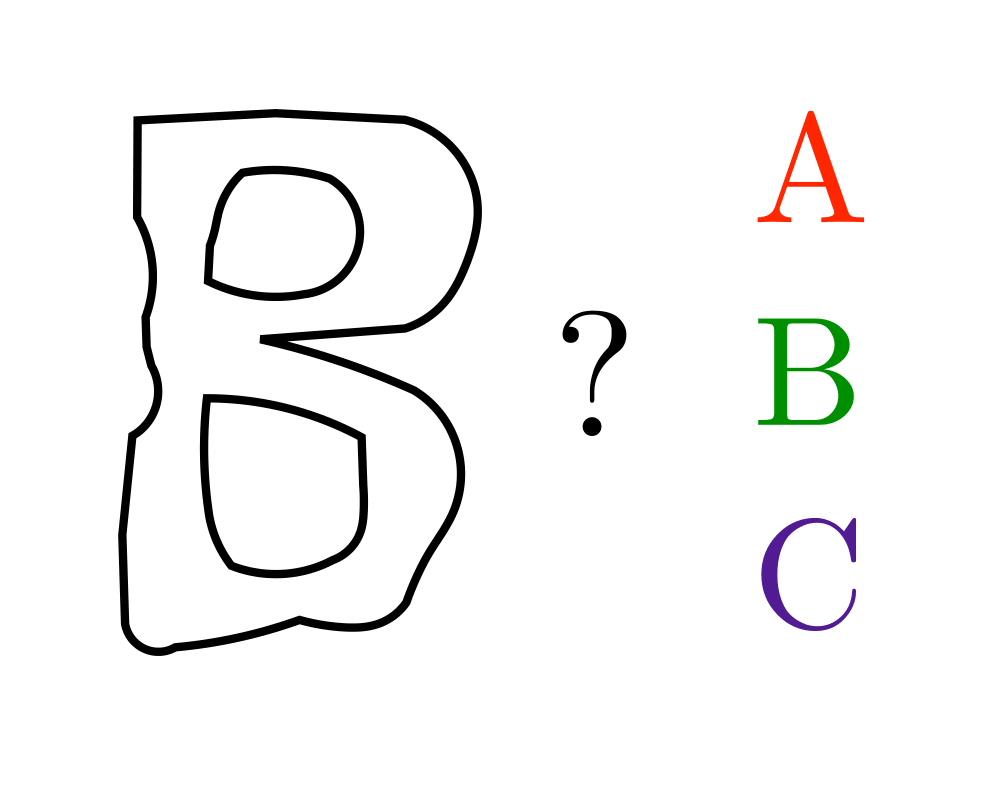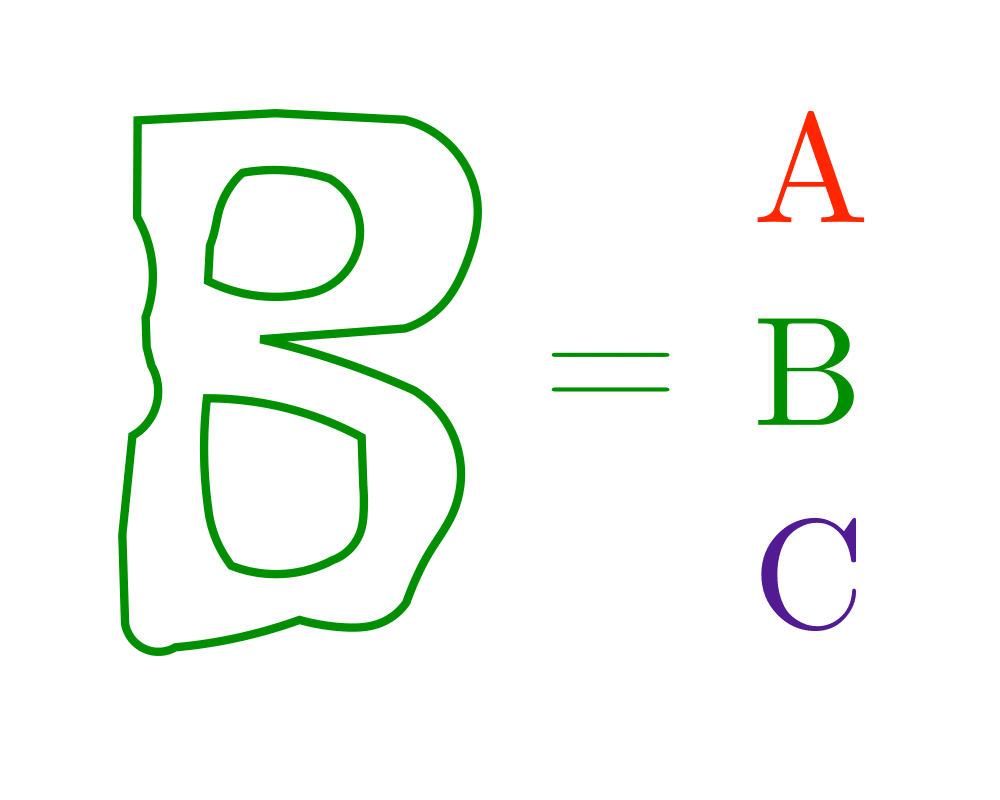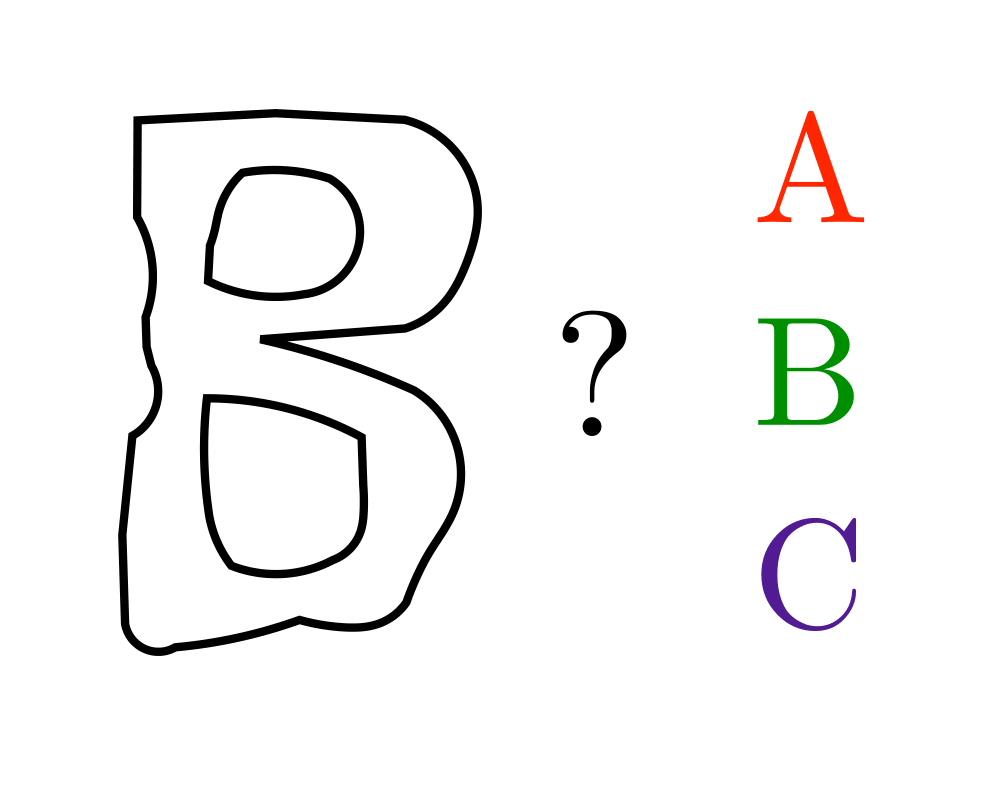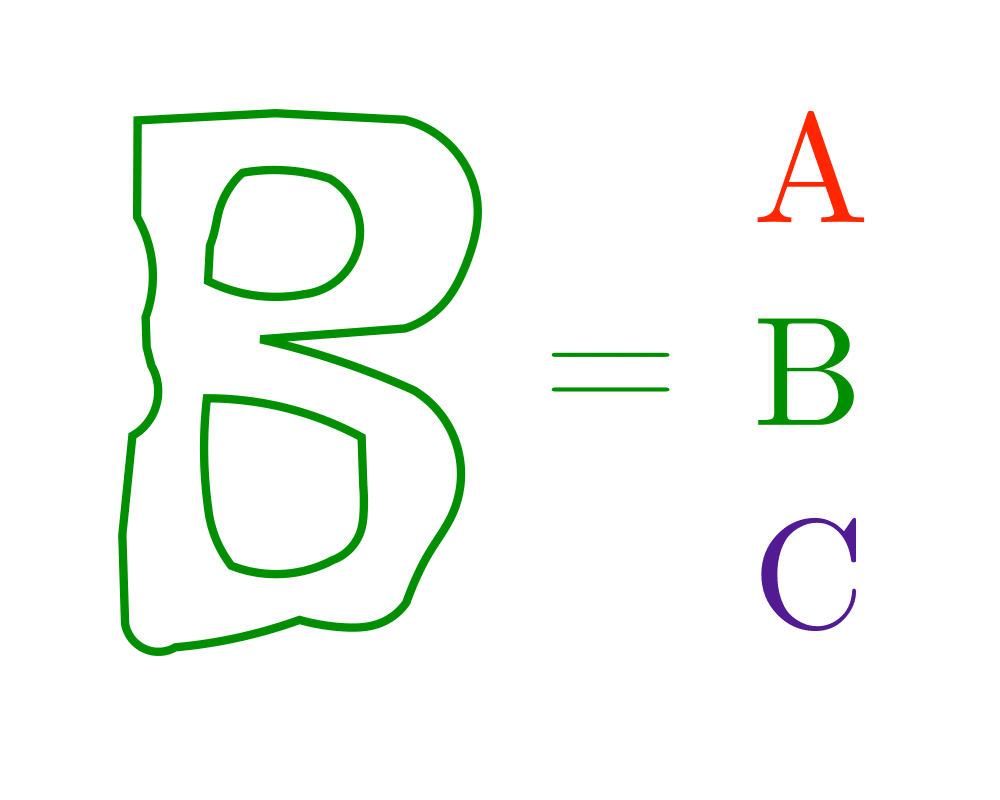 |
 |
|
|
Input Description: Two polygonal shapes, \(P_1\) and \(P_2\).
Problem: How similar are \(P_1\) and \(P_2\)?
Excerpt from The Algorithm Design Manual: Shape similarity is a problem that underlies much of pattern recognition. Consider a system for optical character recognition (OCR). We have a known library of shape models representing letters and the unknown shapes we obtain by scanning a page. We seek to identify an unknown shape by matching it to the most similar shape model.
The problem of shape similarity is inherently ill-defined, because what ``similar'' means is application dependent. Thus no single algorithmic approach can solve all shape matching problems. Whichever method you select, expect to spend a large chunk of time tweaking it so as to achieve maximum performance. Don't kid yourself -- this is a difficult problem.
| Shape similarity testing via turning functions (rating 8) |
SegMatch (rating 8) |
| svmjs (rating 7) |
KML (rating 7) |
| SVMlight (rating 7) |
LIBSVM (rating 7) |
| SNNS (rating 5) |
 Algorithms for Clustering Data by A. Jain and R. Dubes |
 Pattern Classification and Scene Analysis by R. Duda and P. Hart |
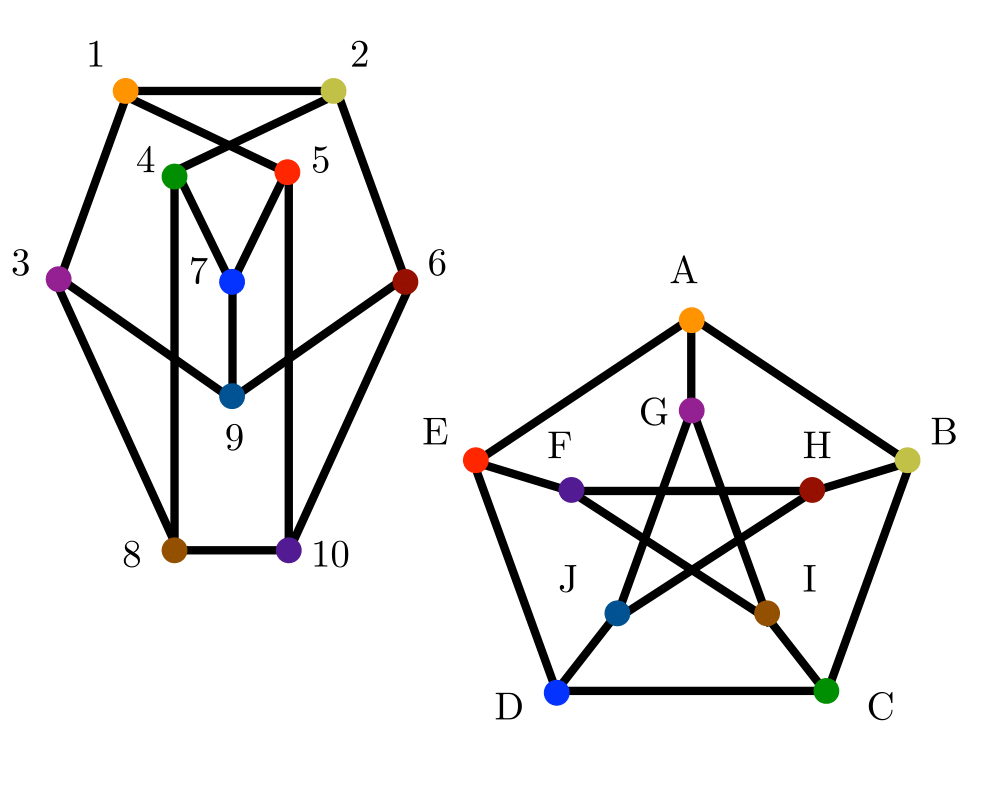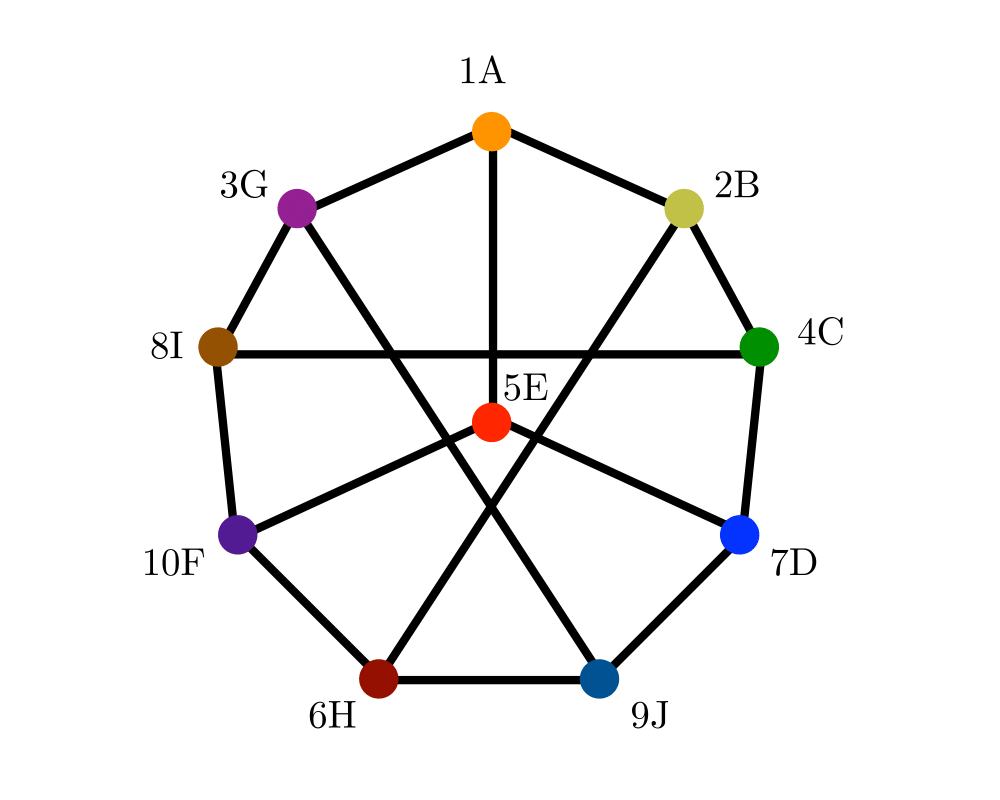  Graph Isomorphism |
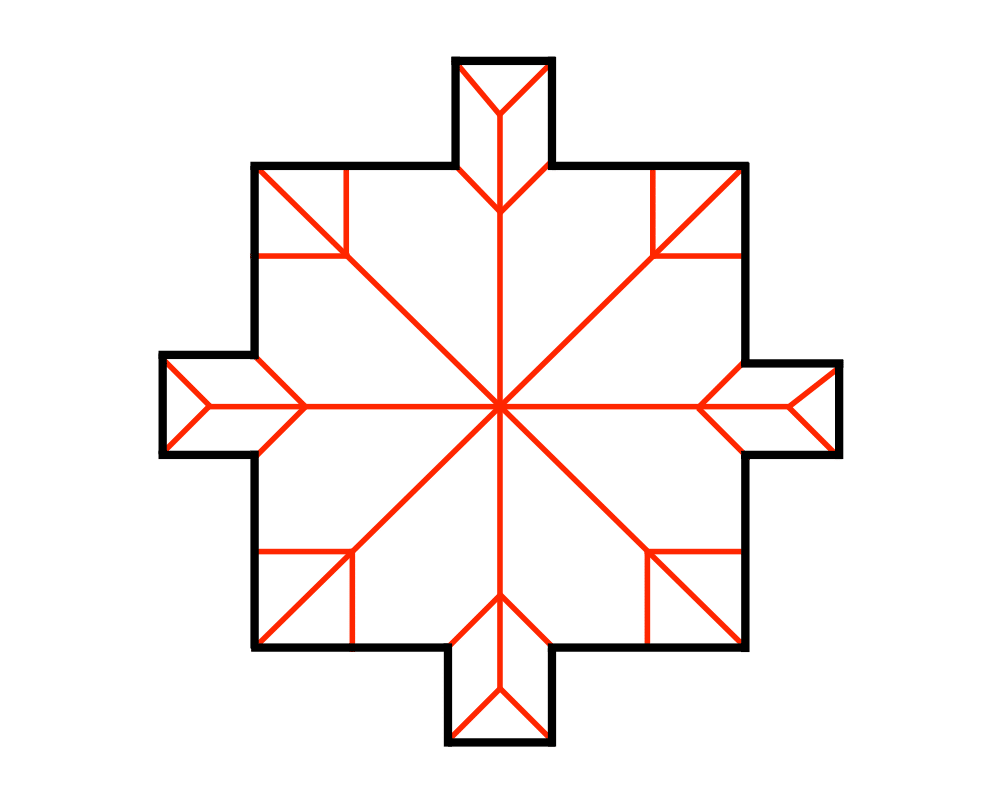  Medial-Axis Transform |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.