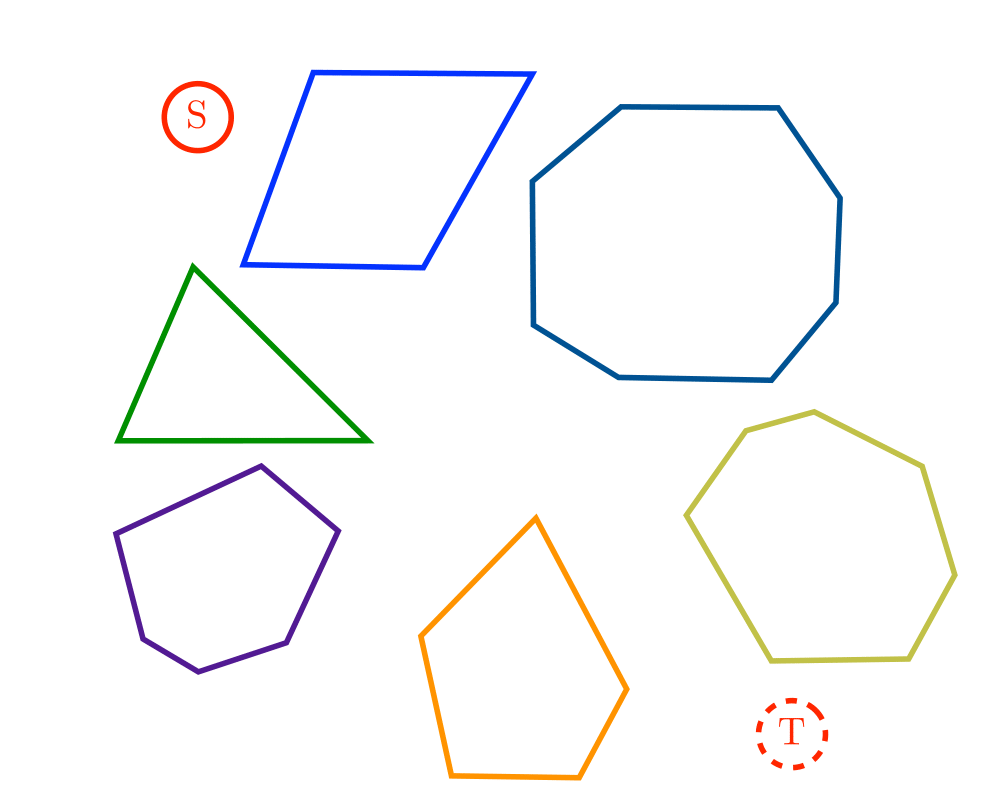
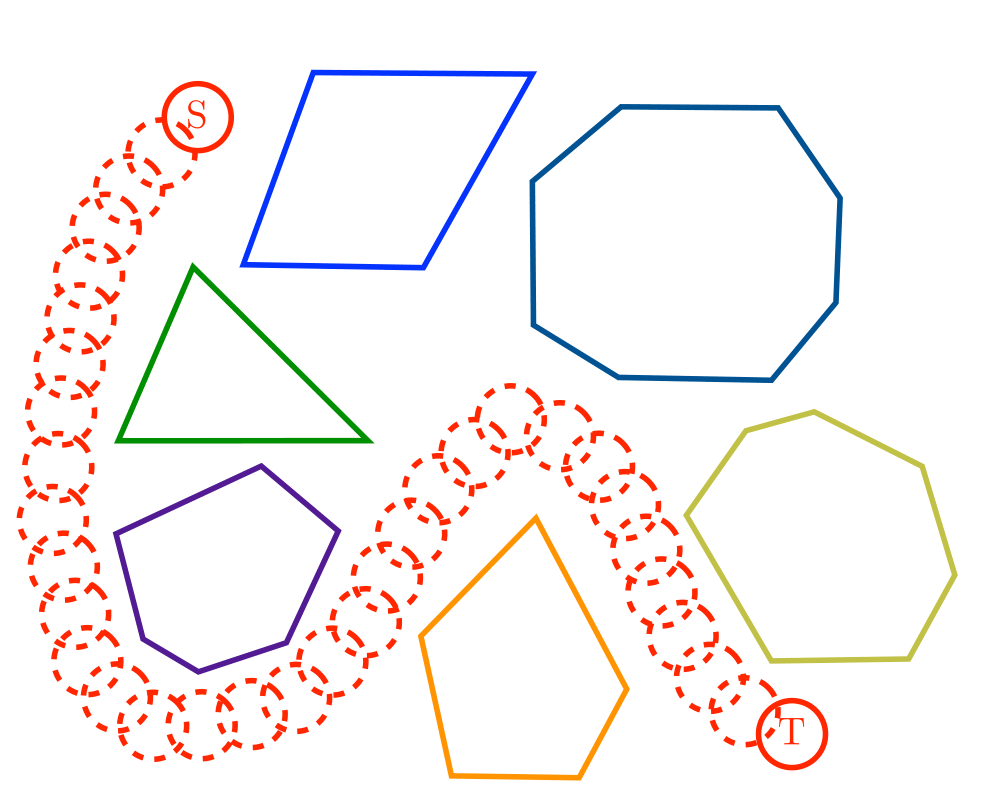
 |
 |
|
|
Input Description: A polygonal-shaped robot \(s\) in a given starting position in a room containing polygonal obstacles, with a desired ending position \(t\).
Problem: Find the shortest path in the room taking \(s\) to \(t\) without going through any of the obstacles.
Excerpt from The Algorithm Design Manual: The difficulty of motion planning will be obvious to anyone who has ever had to move a large piece of furniture into a small apartment. The problem of motion planning also arises in systems for molecular docking. Many drugs are small molecules that act by binding to a given target model. The problem of identifying which binding sites are accessible to a candidate drug is clearly an instance of motion planning. Plotting paths for mobile robots is another canonical motion-planning application.
Motion planning also provides a tool for computer animation. Given a set of object models that appear in two different scenes \(s1\) and \(s2\), a motion planning algorithm can construct a short sequence of intermediate motions to transform \(s1\) to \(s2\). These motions can serve to fill in the intermediate scenes between \(s1\) and \(s2\), with such scene interpolation greatly reducing the amount of work the animator has to do.
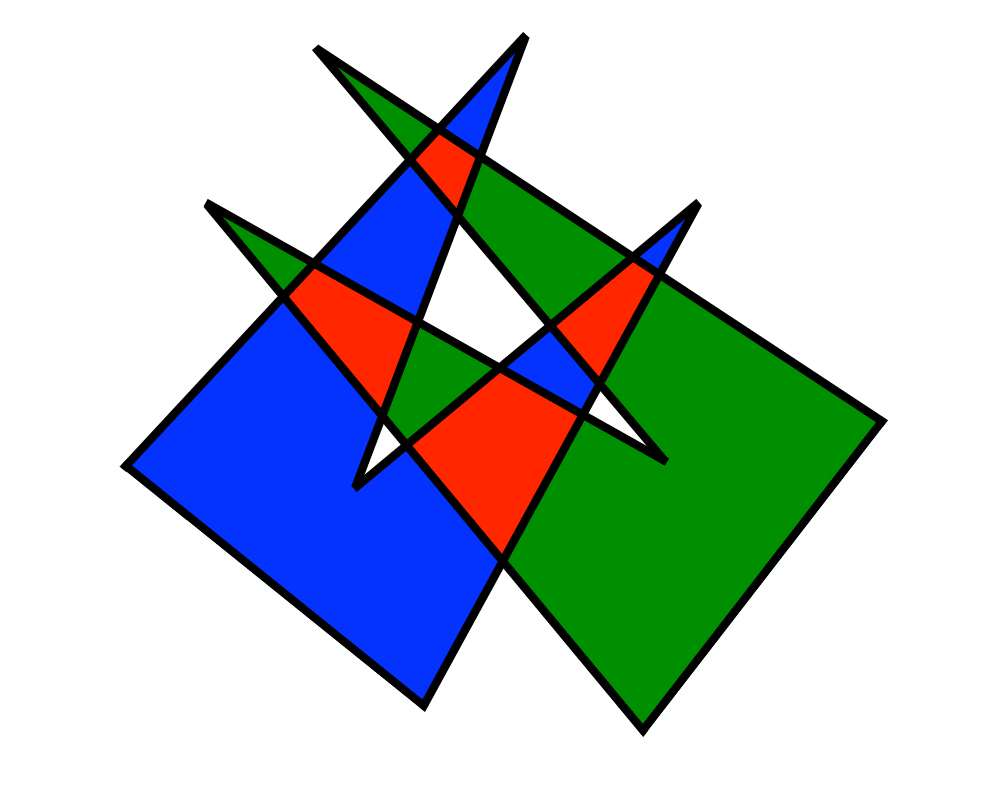  Intersection Detection |
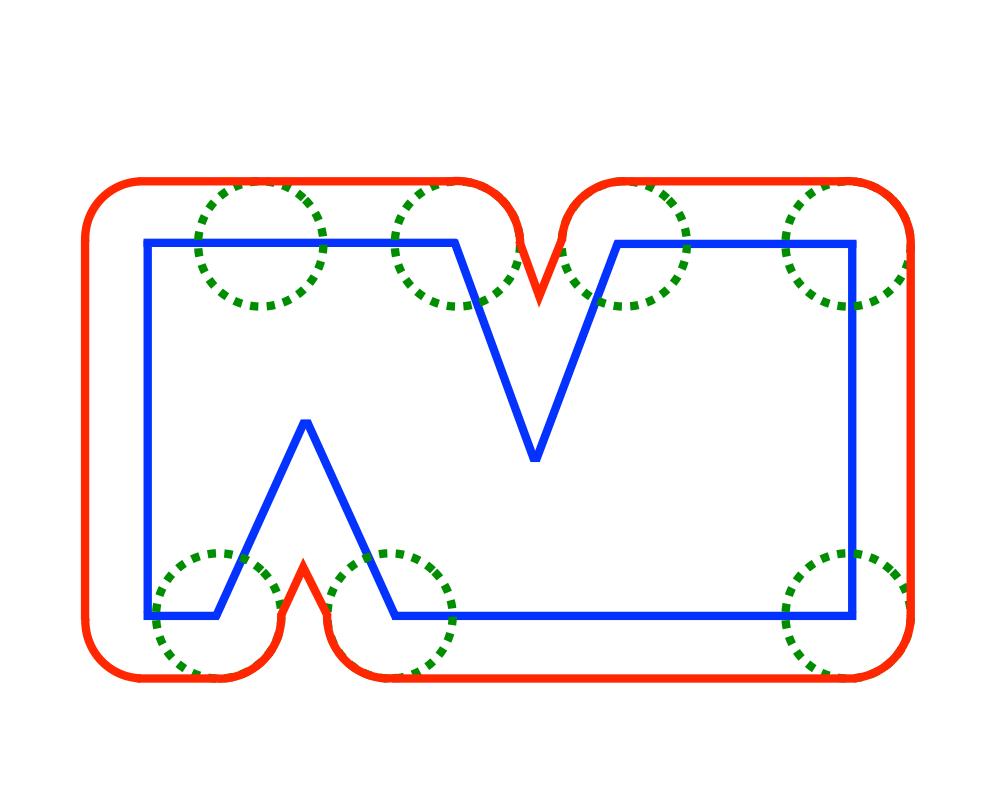  Minkowski Sum |
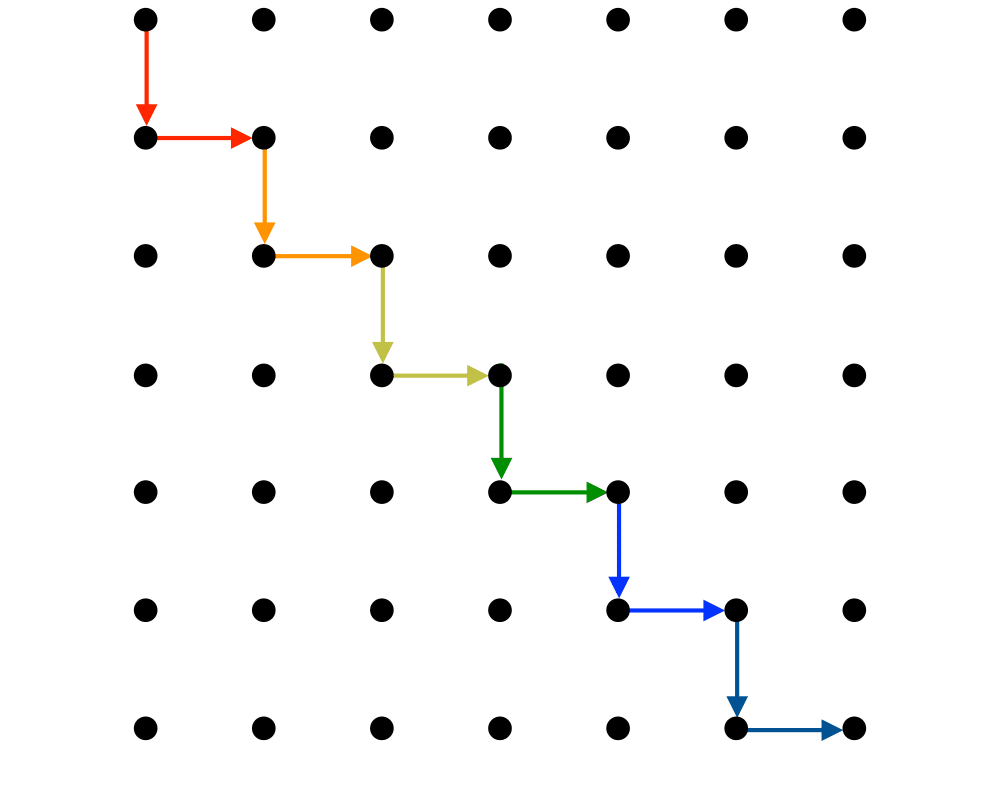  Shortest Path |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
Davenport-Schinzel sequences and their geometric applications by M. Sharir and P. Agarwal
Computational Geometry in C by Joseph O'Rourke
Robot Motion Planning by J.-C. Latombe
Planning, geometry, and complexity of robot motion by J. Hopcroft and J. Schwartz and M. Sharir
The complexity of robot motion planning by J. Canny