 |
 |
|
|
Input Description: A graph \(G=(V,E)\).
Problem: Color the vertices of \(V\) using the minimum number of colors such that \(i\) and \(j\) have different colors for all \((i,j) \in E\).
Excerpt from The Algorithm Design Manual: Vertex coloring arises in many scheduling and clustering applications. Register allocation in compiler optimization is a canonical application of coloring. Each variable in a given program fragment has a range of times during which its value must be kept intact, in particular after it is initialized and before its final use. Any two variables whose life spans intersect cannot be placed in the same register. Construct a graph where each vertex corresponds to a variable, with an edge between any two vertices whose variable life spans intersect. Since none of the variables assigned the same color clash, they all can be assigned to the same register.
No conflicts will occur if each vertex is colored using a distinct color. But computers have a limited number of registers, so we seek a coloring using the fewest colors. The smallest number of colors sufficient to vertex-color a graph is its \(chromatic number\).
  Edge Coloring |
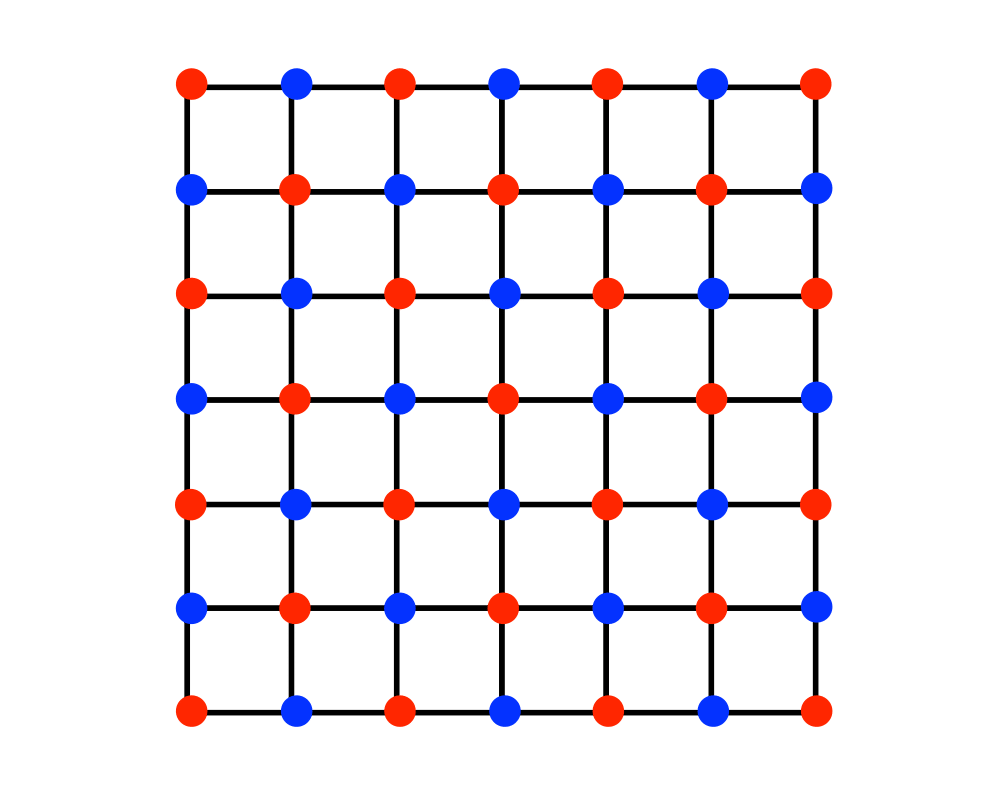  Independent Set |
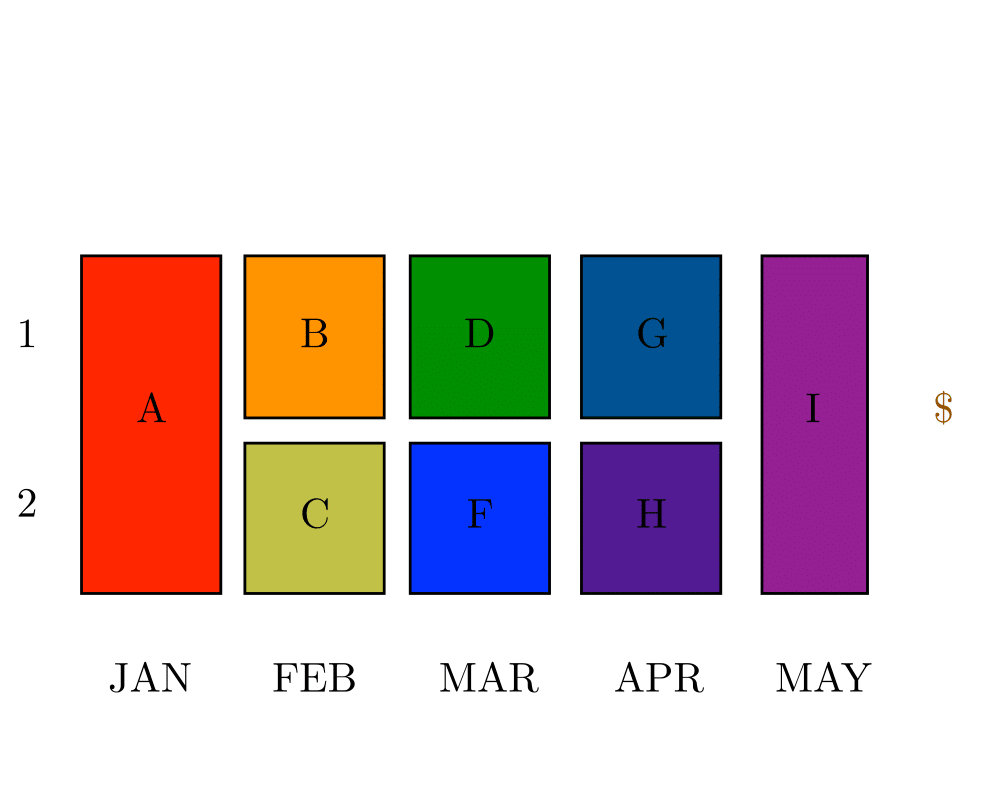  Job Scheduling |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica by S. Pemmaraju and S. Skiena
The Four-Color Problem by T. Saaty and P. Kainen
Combinatorial Algorithms for Computers and Calculators by A. Nijenhuis and H. Wilf