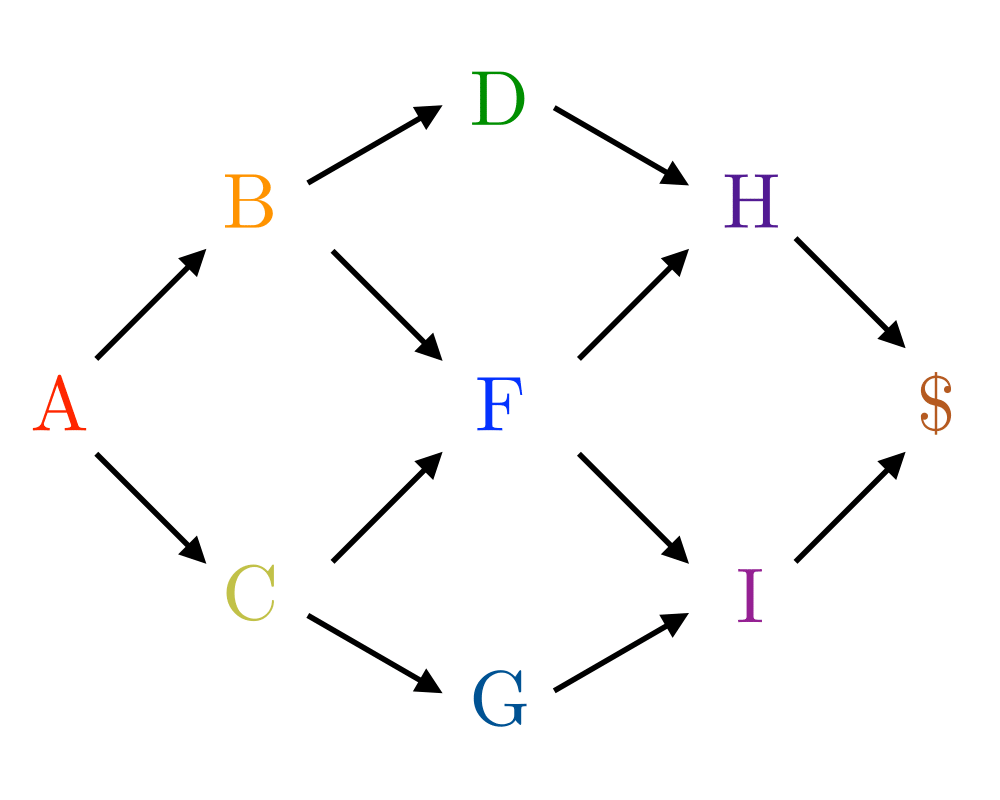
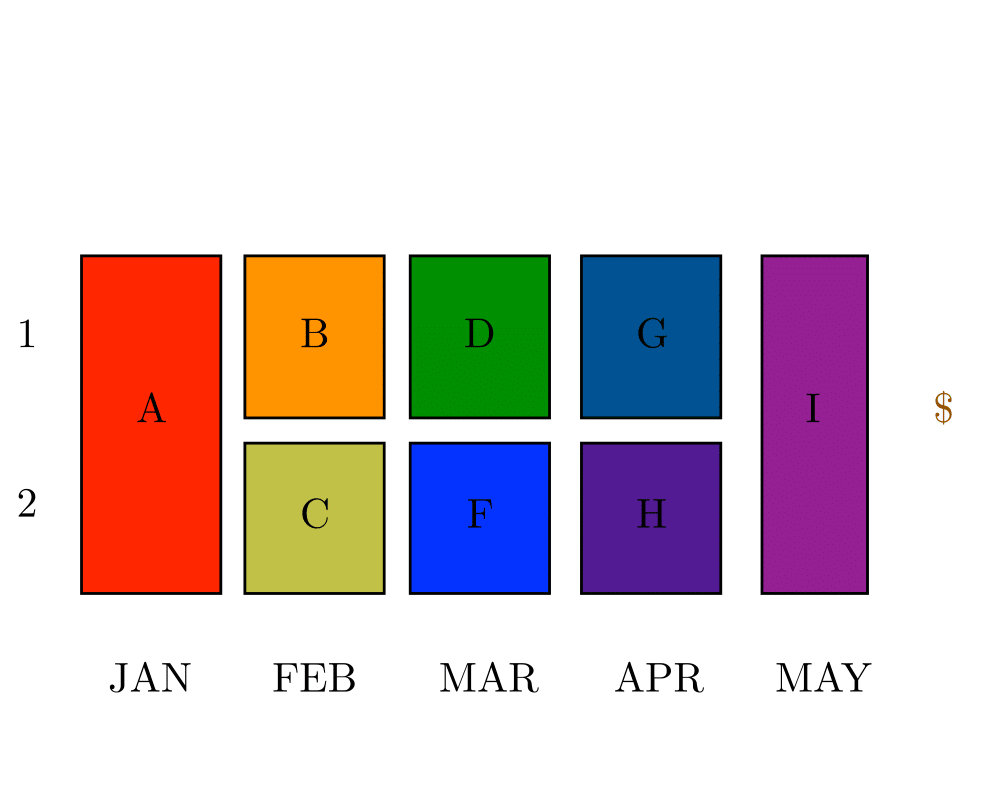
 |
 |
|
|
Input Description: A directed acyclic graph \(G=(V,E)\), where the vertices represent jobs and the the edge \((u,v)\) that task \(u\) must be completed before task \(v\).
Problem: What schedule of tasks to completes the job using the minimum amount of time or processors?
Excerpt from The Algorithm Design Manual: Devising a proper schedule to satisfy a set of constraints is fundamental to many applications. A critical aspect of any parallel processing system is the algorithm mapping tasks to processors. Poor scheduling can leave most of the expensive machine sitting idle while one bottleneck task is performed. Assigning people to jobs, meetings to rooms, or courses to final exam periods are all different examples of scheduling problems.
Scheduling problems differ widely in the nature of the constraints that must be satisfied and the type of schedule desired. For this reason, several other catalog problems have a direct application to various kinds of scheduling.
We focus on precedence-constrained scheduling problems for directed acyclic graphs. These problems are often called PERT/CPM, for Program Evaluation and Review Technique/Critical Path Method. Suppose you have broken a big job into a large number of smaller tasks. For each task you know how long it should take (or perhaps an upper bound on how long it might take). Further, for each pair of tasks you know whether it is essential that one task be performed before another. The fewer constraints we have to enforce, the better our schedule can be. These constraints must define a directed acyclic graph, acyclic because a cycle in the precedence constraints represents a Catch-22 situation that can never be resolved.
| linux (rating 10) |
JOBSHOP (rating 10) |
| Tablix (rating 10) |
luigi (rating 9) |
| nomad (rating 9) |
LEKIN (rating 9) |
| ILOG CP (rating 8) |
Netlib (rating 4) |
| Discrete Optimization Methods (rating 4) |
  Bin Packing |
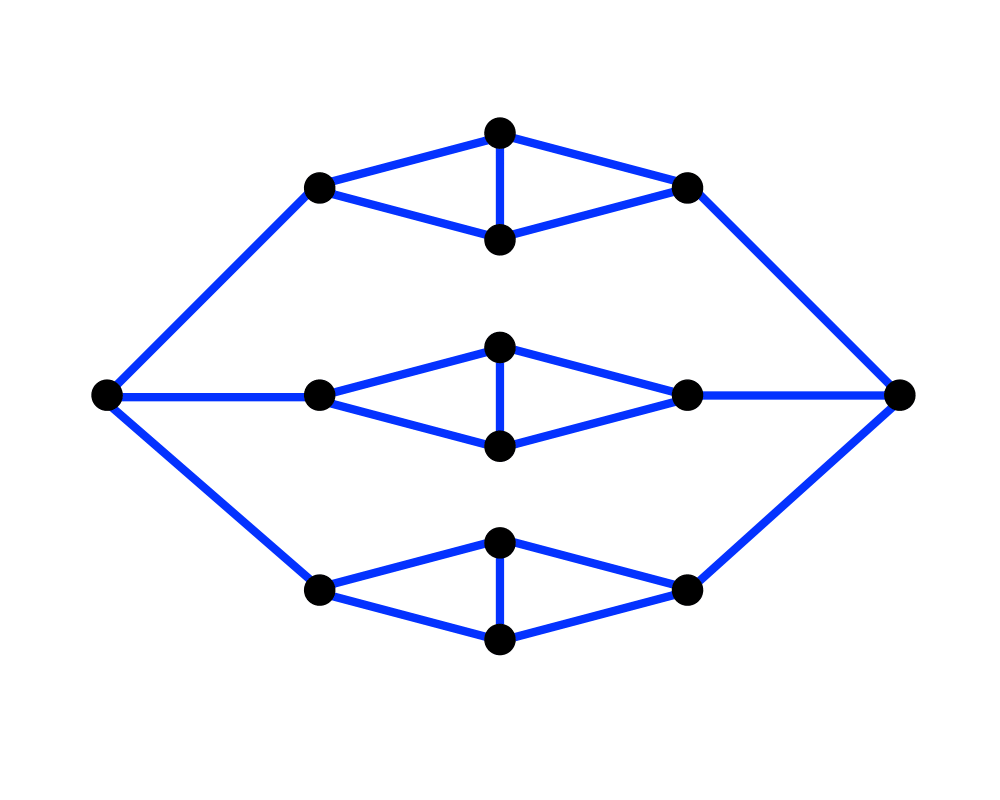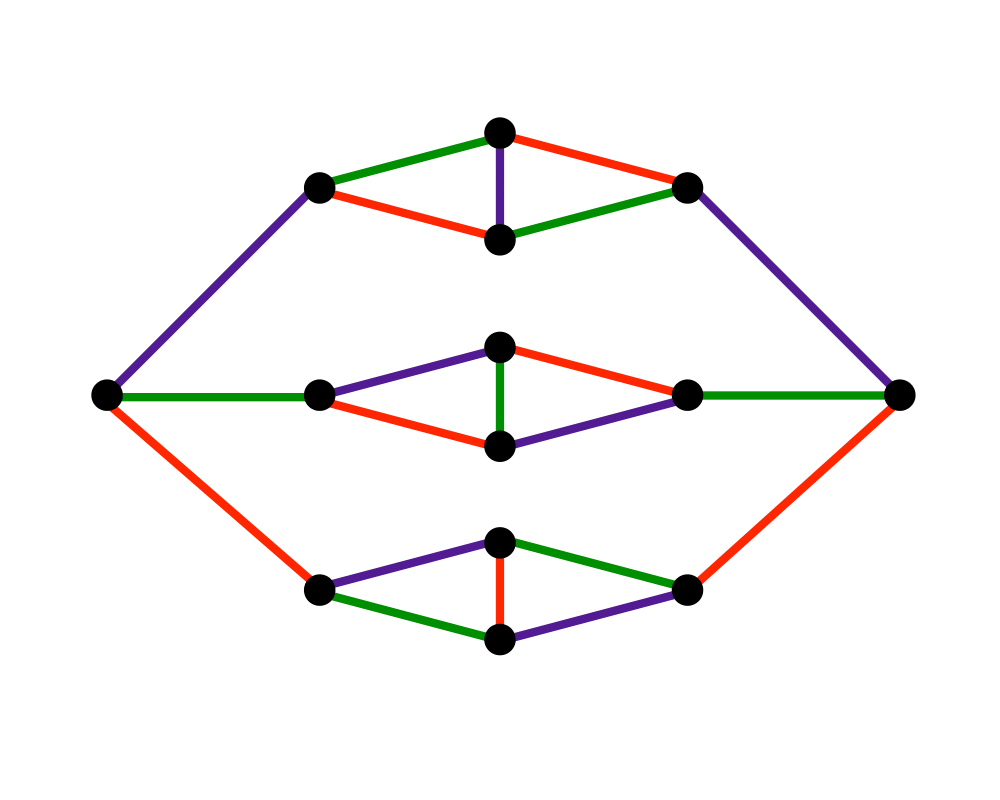  Edge Coloring |
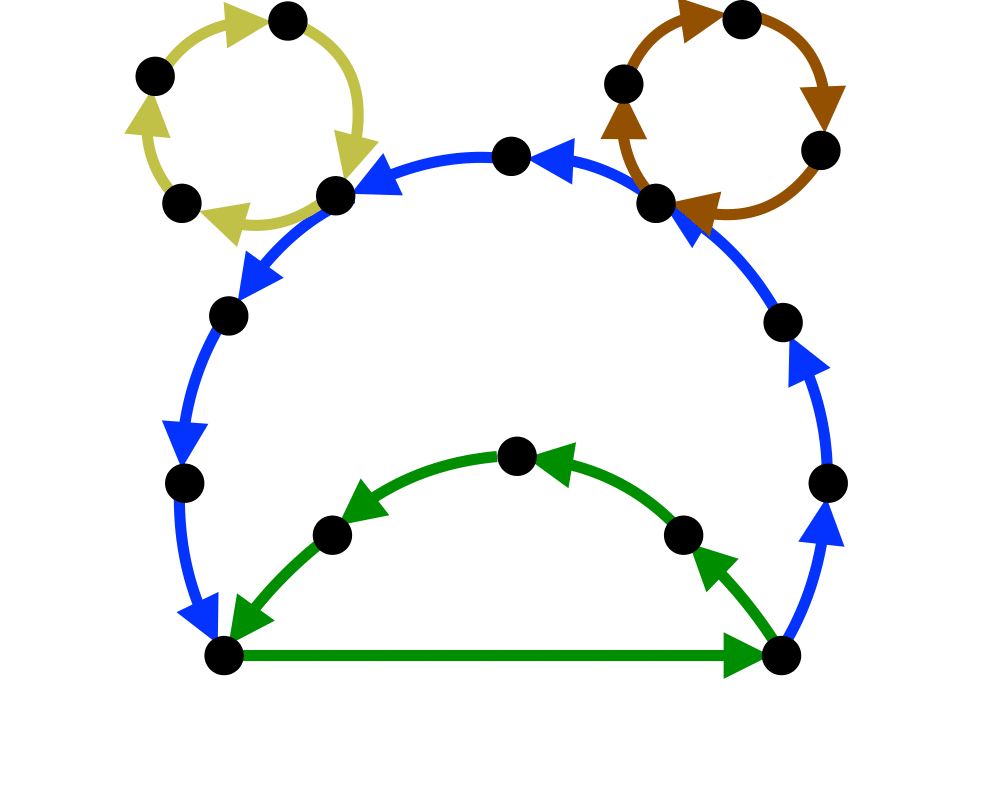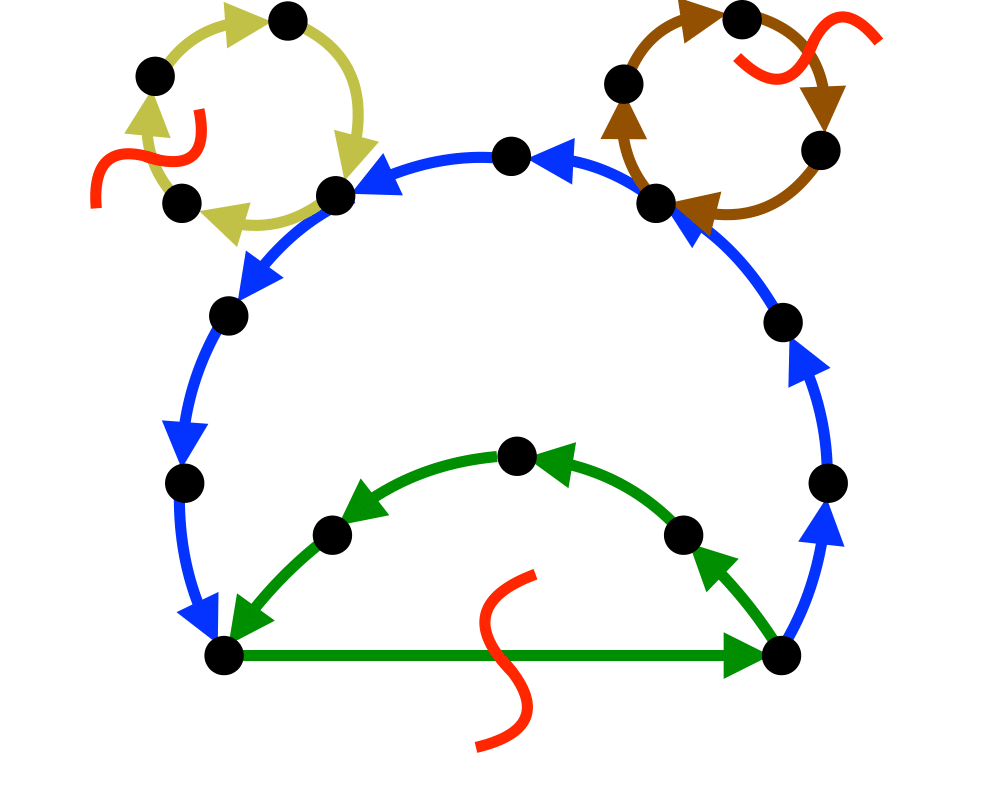  Feedback Edge/Vertex Set |
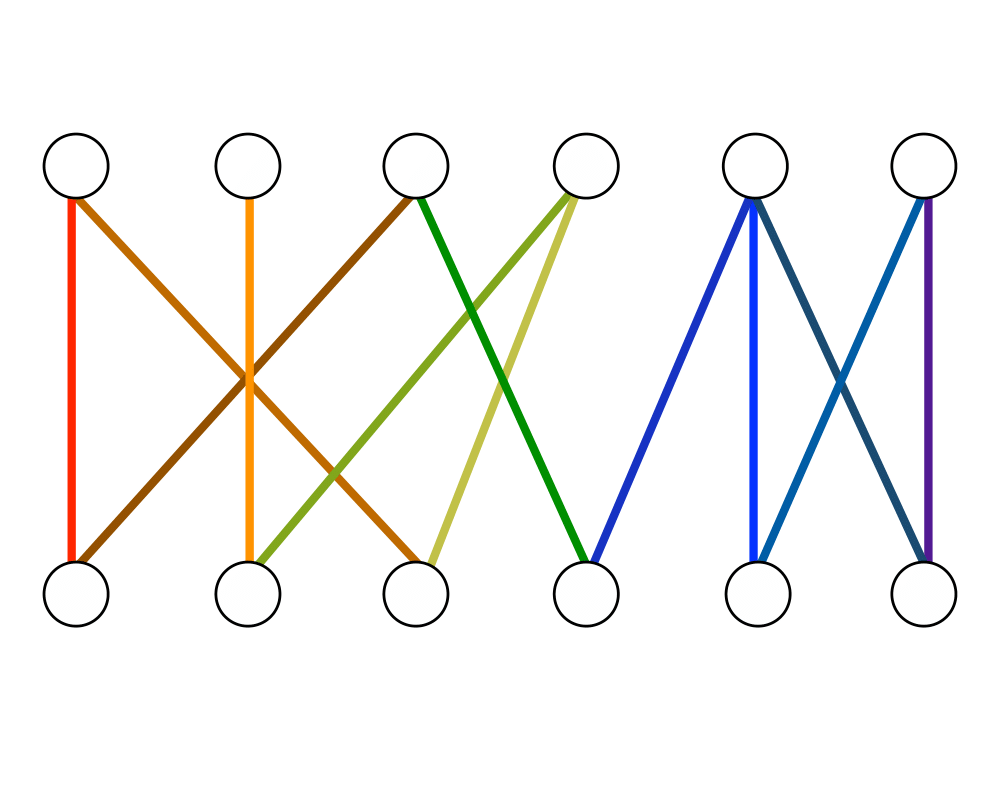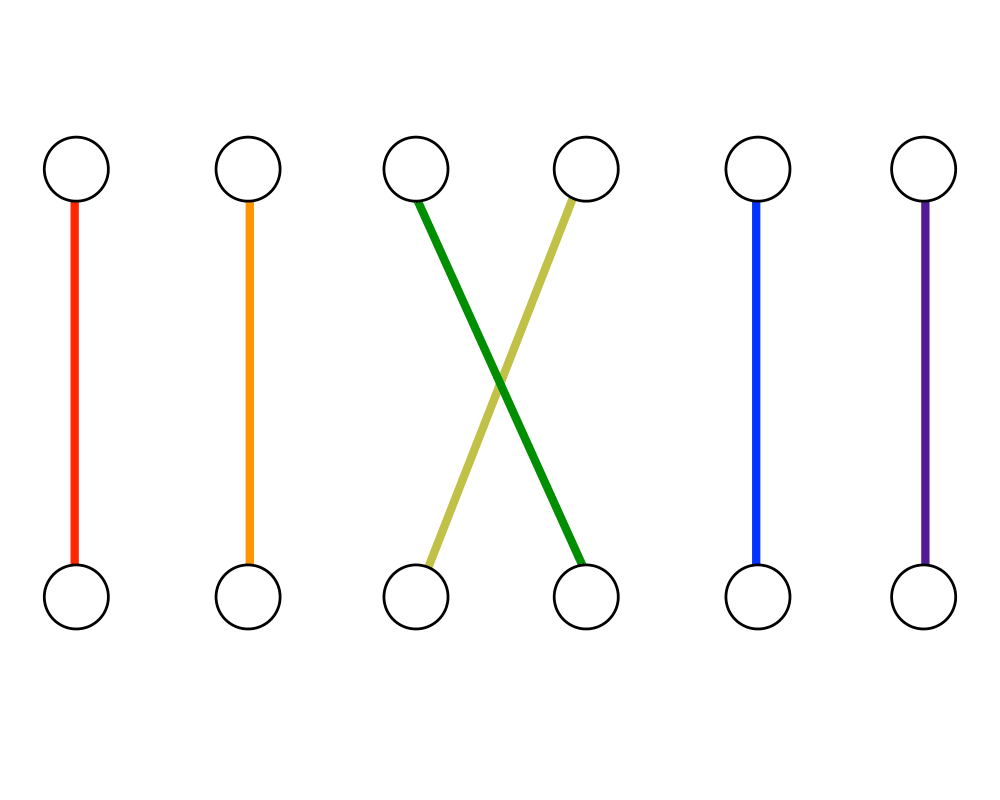  Matching |
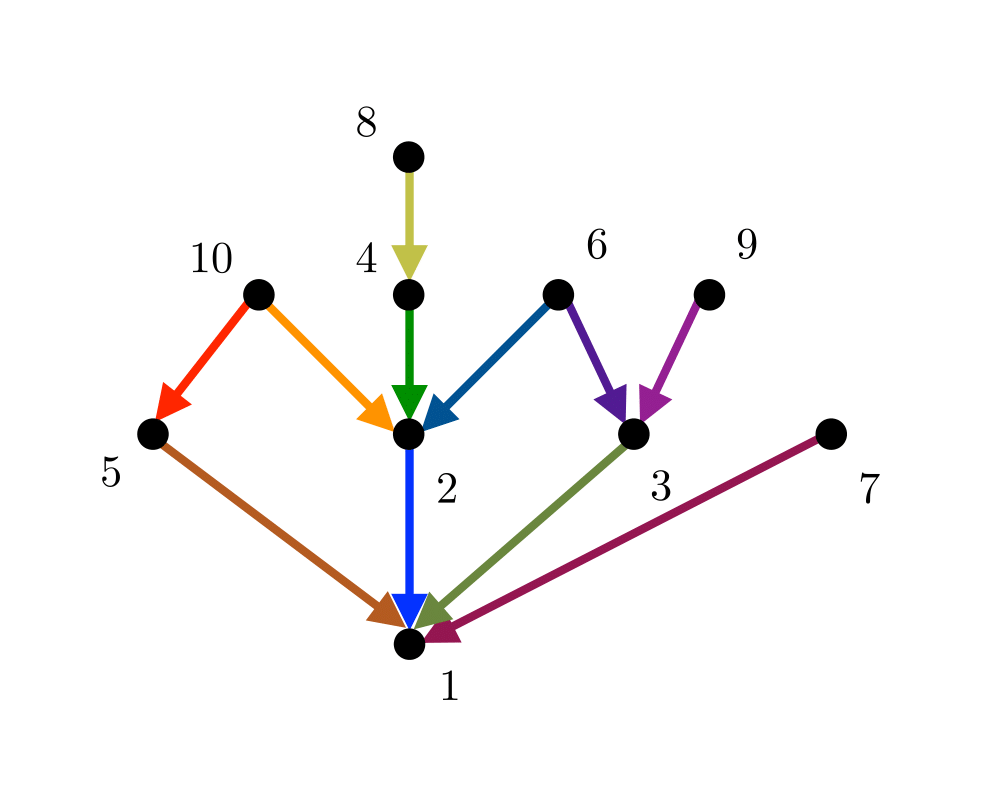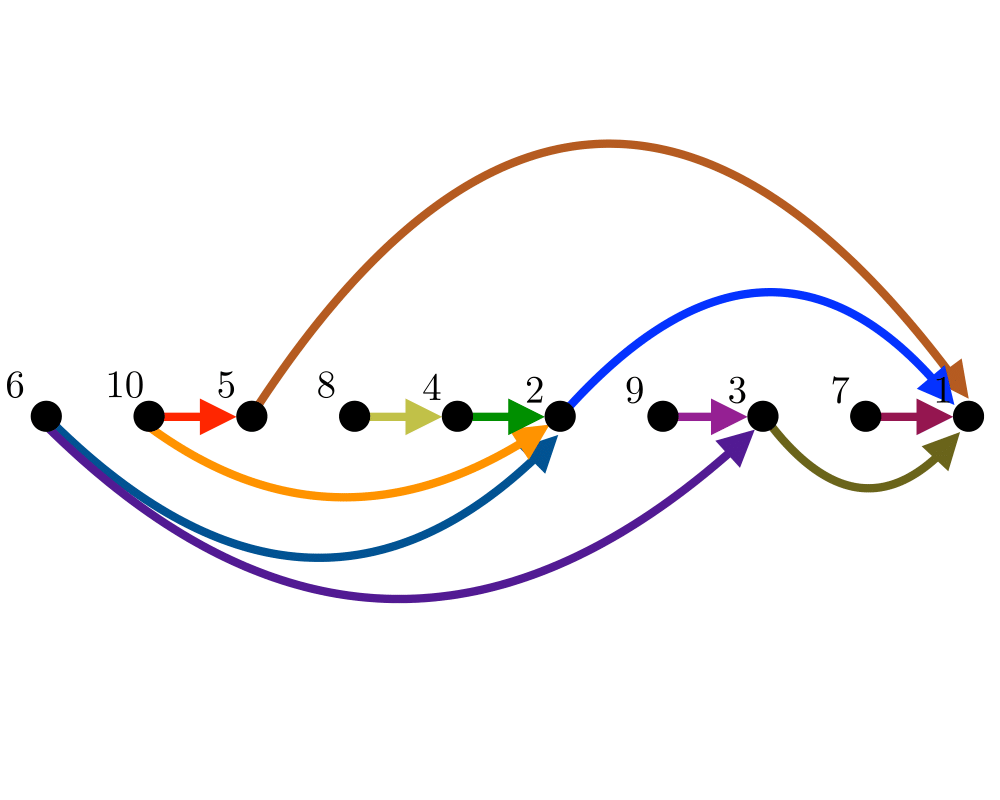  Topological Sorting |
  Vertex Coloring |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
Scheduling Algorithms by P. Brucker
Handbook of Scheduling: Algorithms, Models, and Performance Analysis by Y-T. Leung and James H. Anderson
Scheduling: Theory, Algorithms, and Systems by M. Pinedo
Intelligent Scheduling by Mark Fox