 |
 |
|
|
Input Description: A graph \(G=(V,E)\).
Problem: What is the smallest subset \(S \subset V\) such that each \(e \in E\) contains at least one vertex of \(S\)?
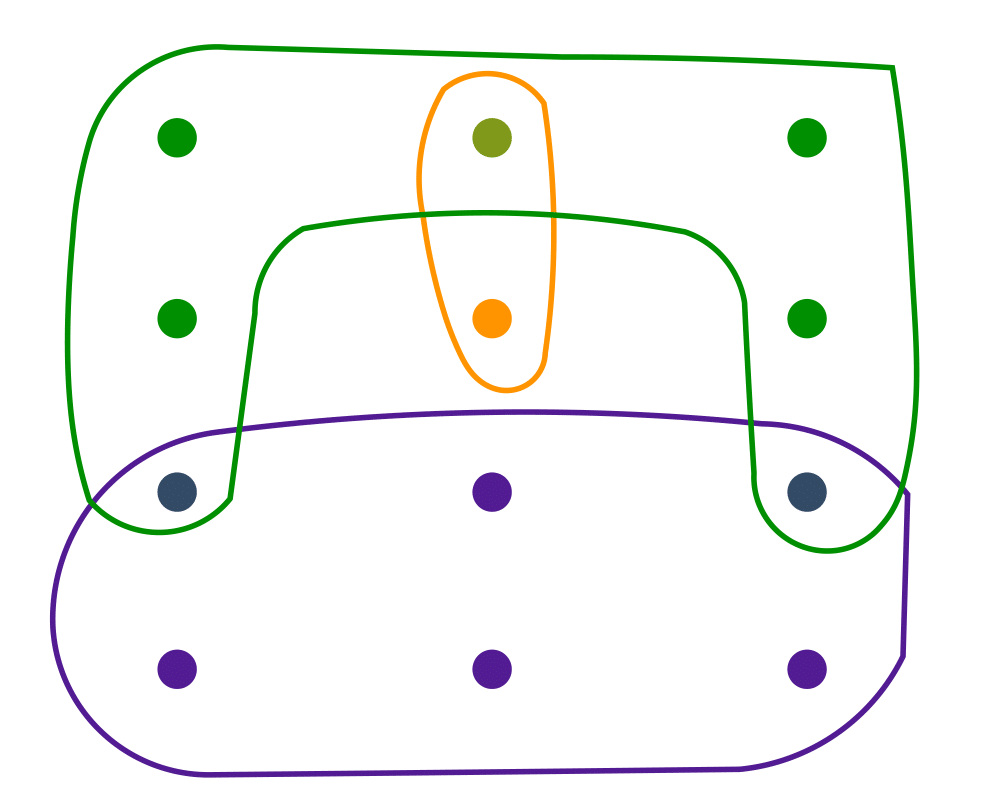
Excerpt from The Algorithm Design Manual: Vertex cover is a special case of the more general set cover problem, which takes as input an arbitrary collection of subsets \(S = (S_1, \ldots, S_n)\) of the universal set \(U = \{1,\ldots,m\}\). We seek the smallest subset of subsets from \(S\) whose union is \(U\). Set cover arises in many applications, including Boolean logic minimization.
To turn vertex cover into a set cover problem, let \(U\) be the complete set of edges, and create \(S_i\) to be the set of edges incident on vertex \(i\). A set of vertices defines a vertex cover in graph \(G\) iff the correspondinag subsets define a set cover in the given instance. However, since each edge can be in only two different subsets, vertex cover instances are simpler than general set cover. The primary reason for distinguishing between the two problems is that vertex cover is a relative lightweight among NP-complete problems, and so can be effectively solved.
| JGraphT (rating 10) |
Neural-Networks for Cliques and Coloring (rating 5) |
| RAPID (rating 4) |
Combinatorica (rating 4) |
 Approximation Algorithms by V. Vazirani |
 Approximation Algorithms for NP-hard Problems by Dorit Hochbaum |
 Combinatorial Optimization: Algorithms and Complexity by C. Papadimitriou and K. Steiglitz |
  Clique |
  Independent Set |
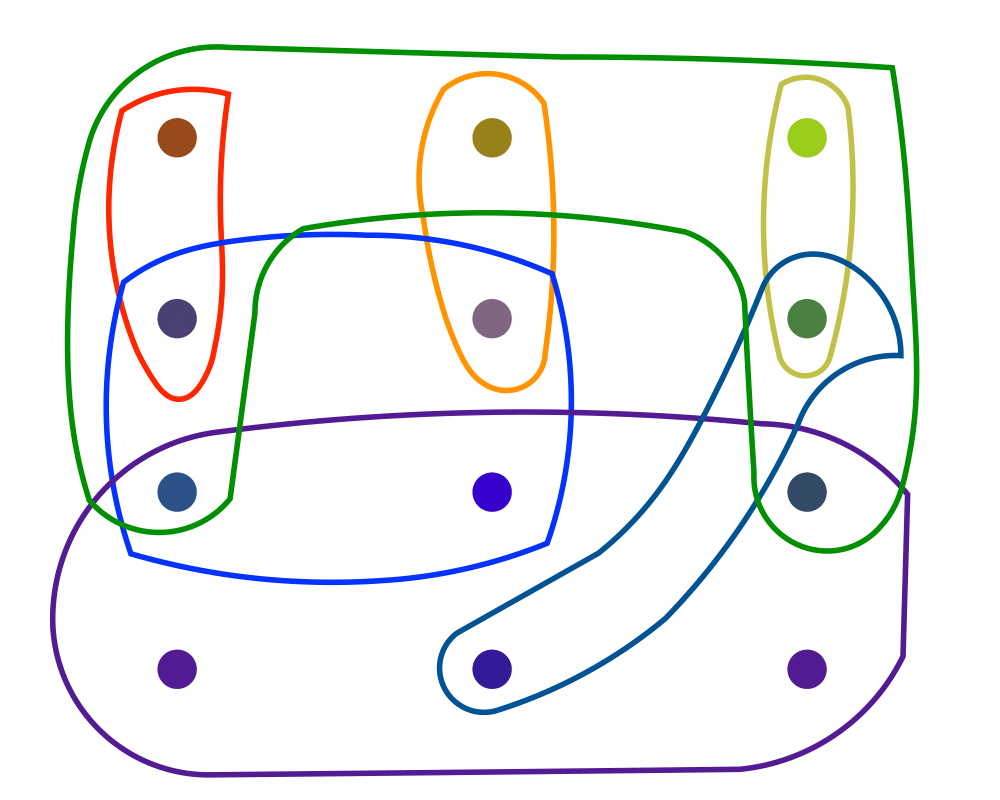  Set Cover |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.