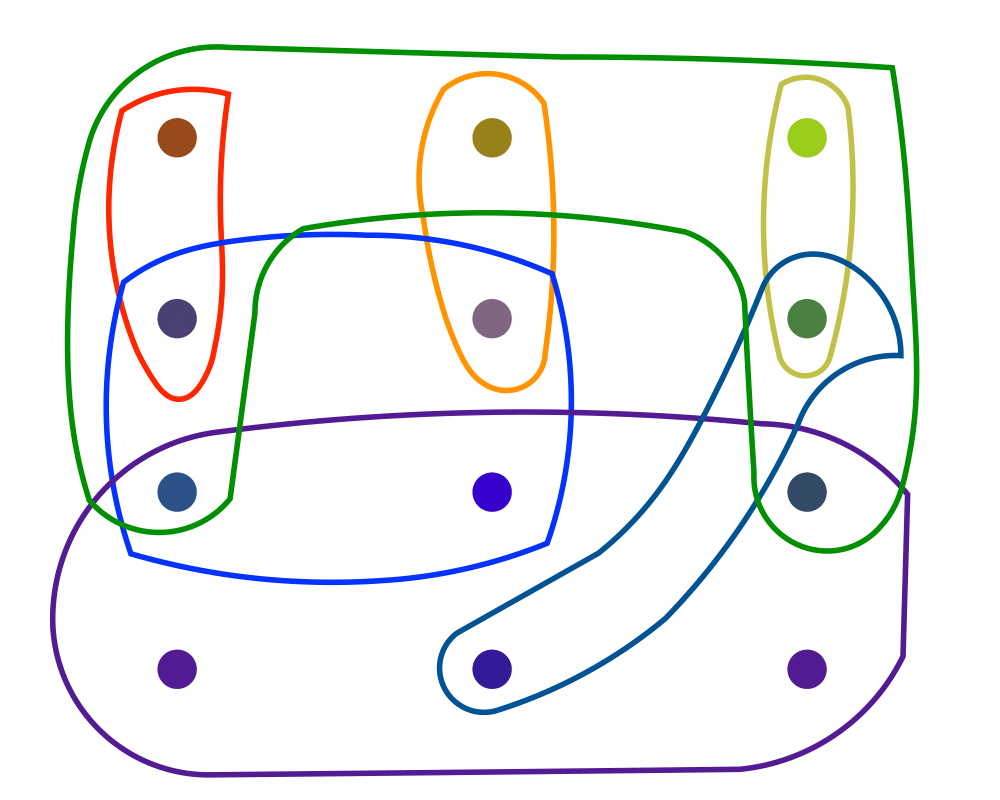
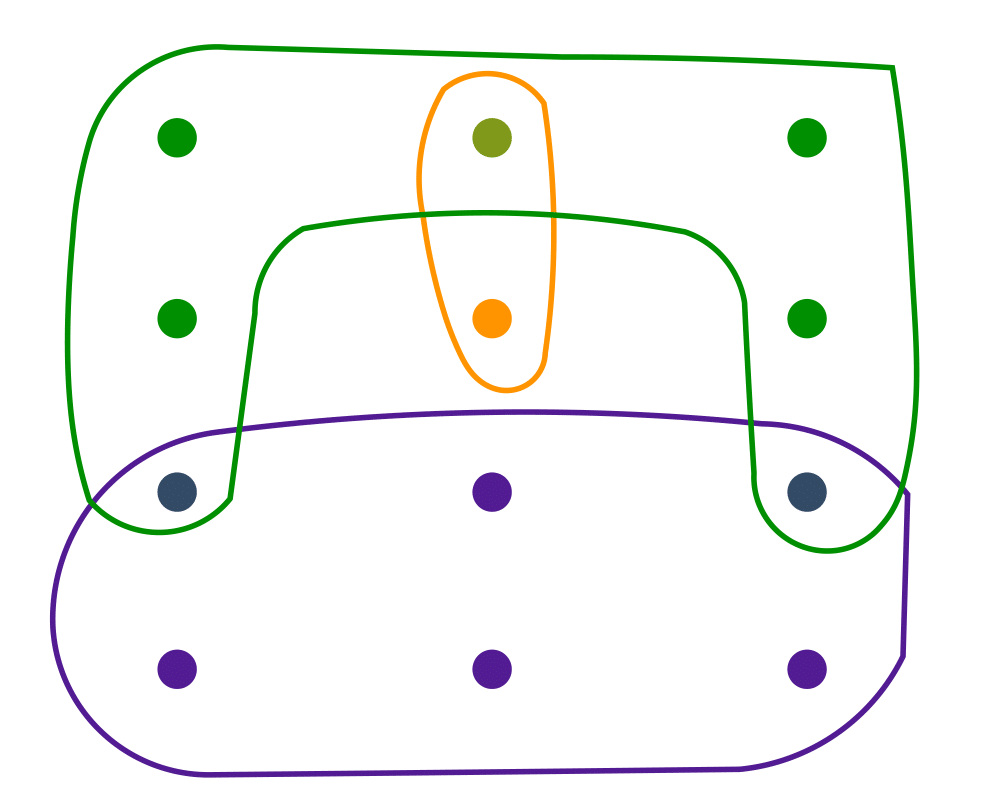
 |
 |
|
|
Input Description: A set of subsets \(S_1, ..., S_m\) of the universal set \(U = \{1,...,n\}\).
Problem: What is the smallest subset of subsets \(T \subset S\) such that \(\cup_{t_i \in T} t_i = U\)?
Excerpt from The Algorithm Design Manual: Set cover arises when you try to efficiently acquire or represent items that have been packaged in a fixed set of lots. You want to obtain all the items, while buying as few lots as possible. Finding a cover is easy, because you can always buy one of each lot. However, by finding a small set cover you can do the same job for less money.
An interesting application of set cover is Boolean logic minimization. We are given a particular Boolean function of \(k\) variables, which for each of the \(2k\) possible input vectors describes whether the desired output is \(0\) or \(1\). We seek the simplest circuit that exactly implements this function. One approach is to find a disjunctive normal form (DNF) formula on the variables and their complements, such as \(x1 \bar x2 + \bar{x}1 \bar{x}2\). We could build one ``and'' term for each input vector and then ``or'' them all together, but we might save considerably by factoring out common subsets of variables. Given a set of feasible ``and'' terms, each of which covers a subset of the vectors we need, we seek to ``or'' together the smallest number of terms that realize the function. This is exactly the set cover problem.
| setcover (rating 6) |
SetCoverPy (rating 6) |
| SYMPHONY (rating 6) |
Discrete Optimization Methods (rating 6) |
  Matching |
  Polygon Partitioning |
  Set Data Structures |
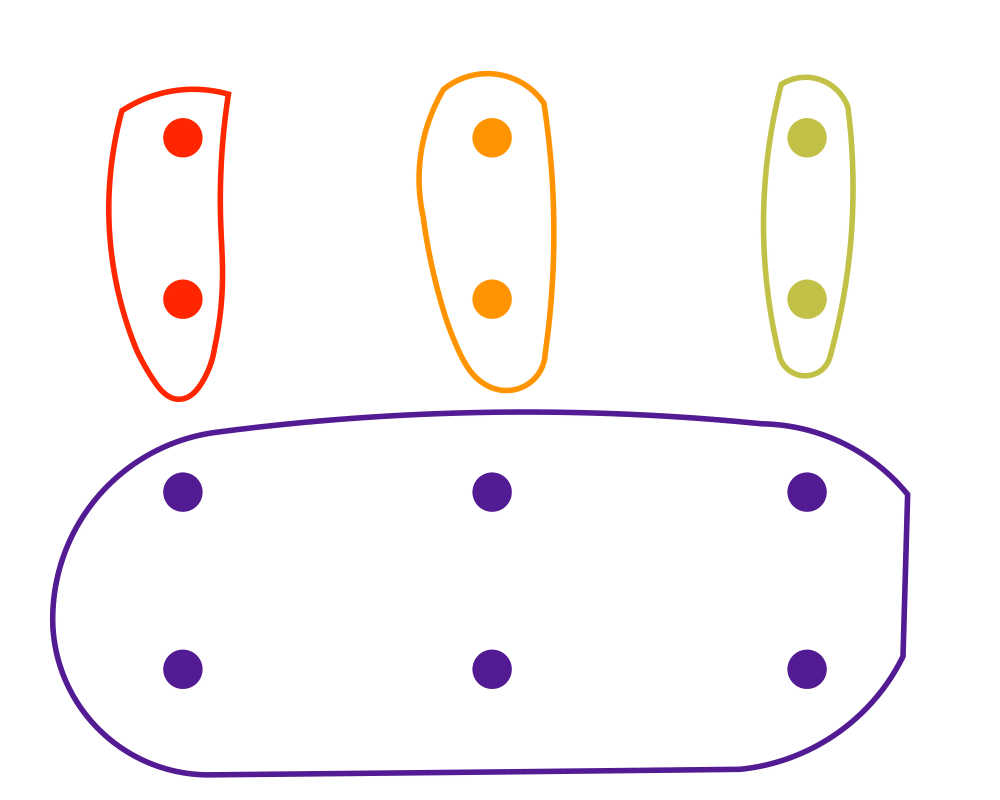  Set Packing |
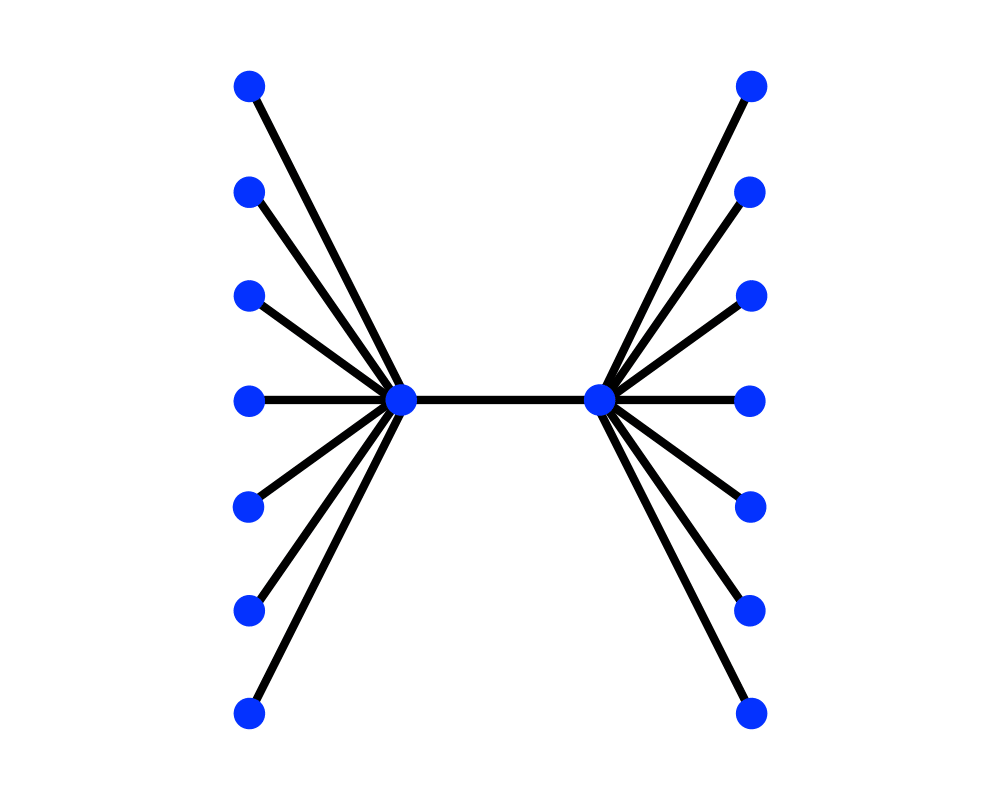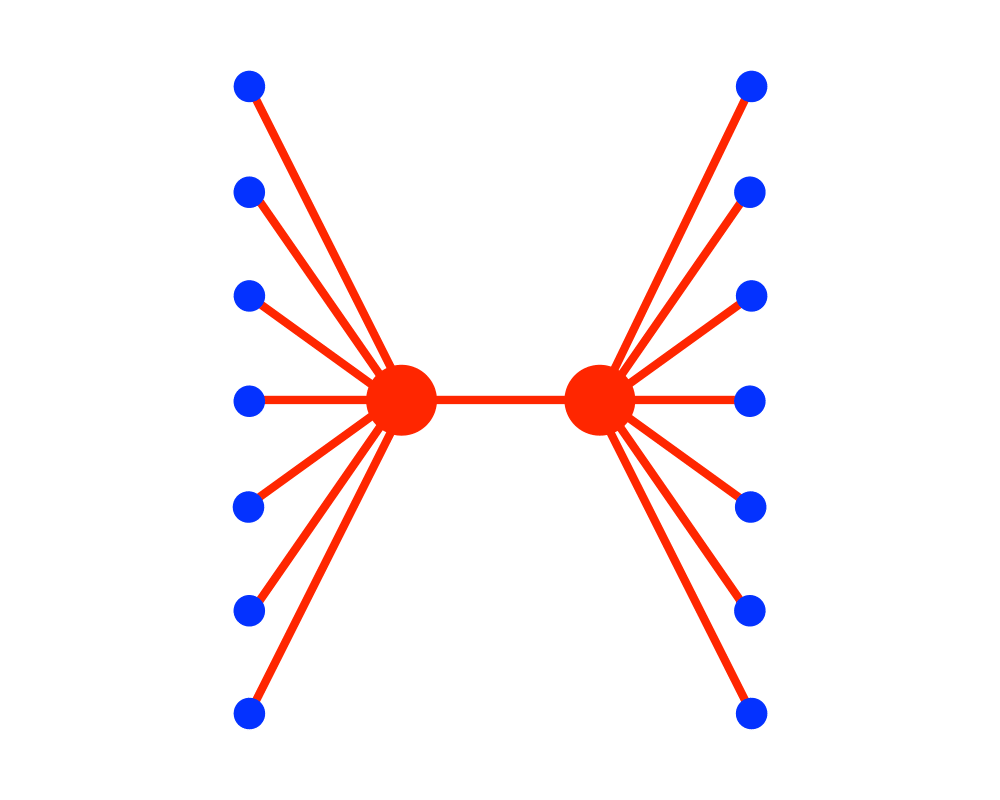  Vertex Cover |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
Introduction to Algorithms by T. Cormen and C. Leiserson and R. Rivest and C. Stein
Discrete Optimization Algorithms with Pascal Programs by M. Syslo and N. Deo and J. Kowalik
Combinatorial Optimization: Algorithms and Complexity by C. Papadimitriou and K. Steiglitz