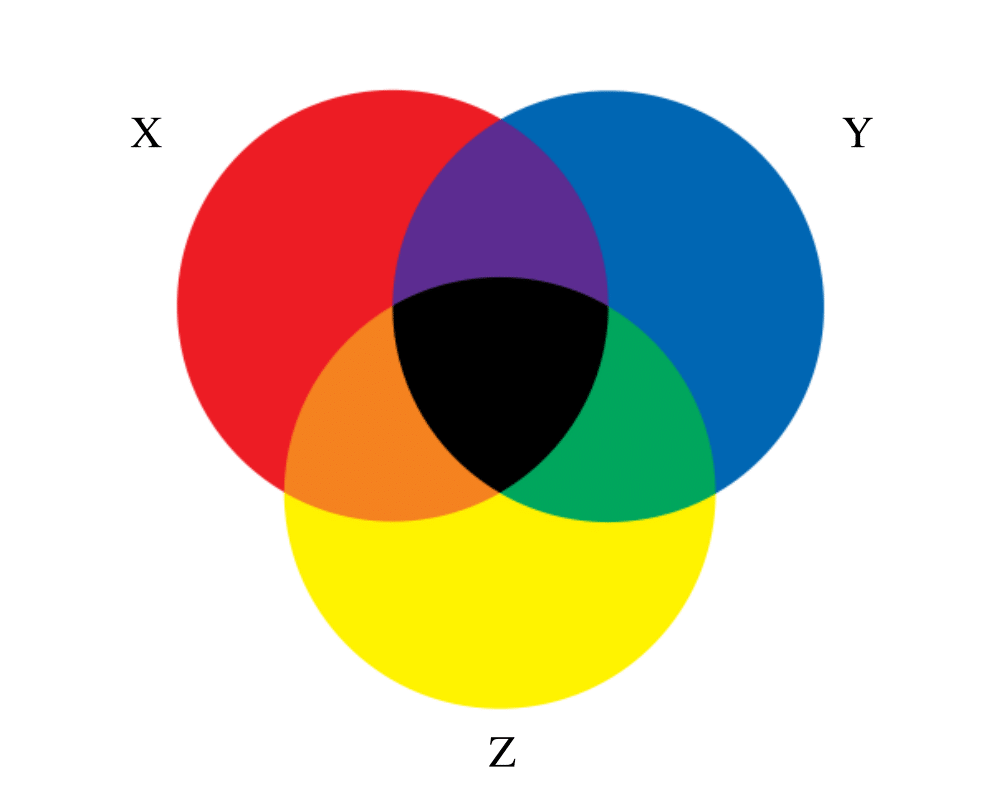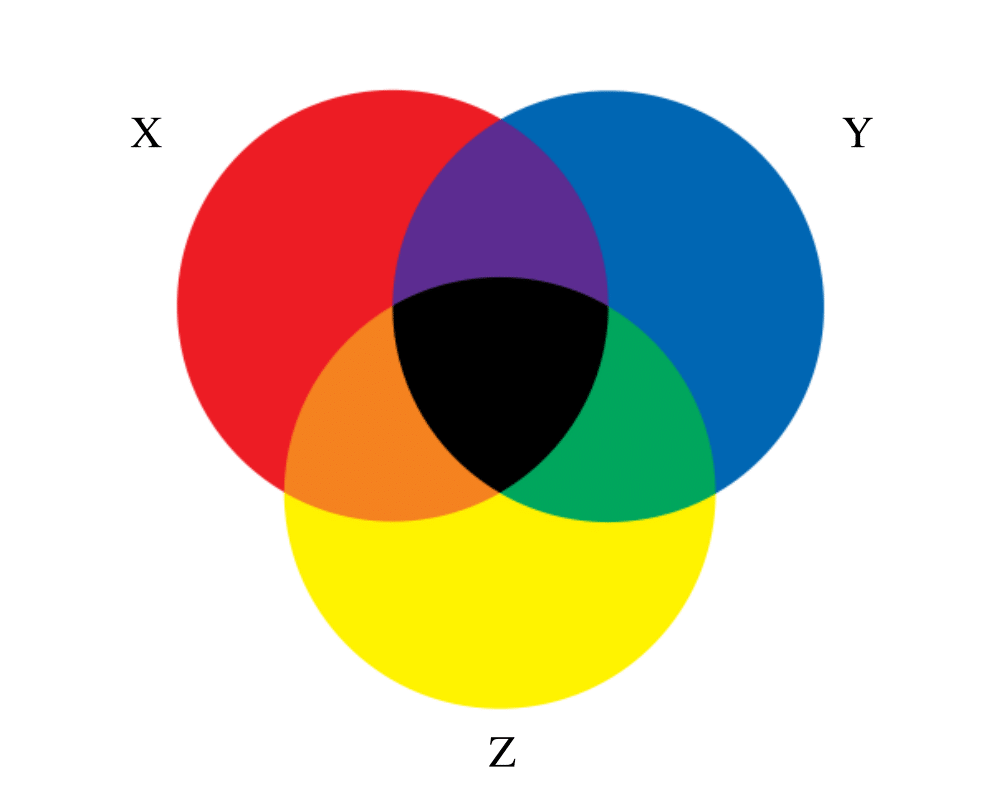Input

Output

Input Description: A universe of objects \(U = \{ u_1,...,u_n\}\), and a collection of subsets \(S_1,...,S_m\), \(S_i \subset U\).
Problem: Represent each subset so as to efficiently (1) test whether \(u_i \in S_j\), (2) find the union or intersection of \(S_i\) and \(S_j\), (3) insert or delete members of \(S_i\).

Excerpt from The Algorithm Design Manual: We distinguish sets from two other kinds of objects: strings and dictionaries. If there is no fixed-size universal set, a collection of objects is best thought of as a dictionary. If the order does matter in a subset, i.e. if {A,B,C} is not the same as {B,C,A}, then your structure is more profitably thought of as a string.

When each subset has cardinality exactly two, they form edges in a graph whose vertices are the universal set. A system of subsets with no restrictions on the cardinality of its members is called a hypergraph. It often can be profitable to consider whether your problem has a graph-theoretical analogy, like connected components or shortest path in a hypergraph.

Your primary alternatives for representing arbitrary systems of subsets are:

• Bit Vectors If your universal set U contains n items, an n-bit vector or array can represent any subset S subset of U. Bit i will be 1 if i is contained in S, otherwise bit i is 0. Since only one bit is used per element, bit vectors can be very space efficient for surprisingly large values of |U|. Element insertion and deletion simply flips the appropriate bit. Intersection and union are done by ``and-ing'' or ``or-ing'' the bits together. The only real drawback of a bit vector is that for sparse subsets, it takes O(n) time to explicitly identify all members of S.
• Containers or dictionaries A subset can also be represented using a linked list, array, binary tree, or dictionary containing exactly the elements in the subset. No notion of a fixed universal set is needed for such a data structure. For sparse subsets, dictionaries can be more space and time efficient than bit vectors and easier to work with and program. For efficient union and intersection operations, it pays to keep the elements in each subset sorted, so a linear-time traversal through both subsets identifies all duplicates.

Implementations

Guava (rating 10)	Python Standard Library (rating 10)
libstdc++ (rating 10)	libc++ (rating 10)
OpenJDK 10 (rating 10)	C++ STL (rating 10)
Guava (rating 9)	Java Collections (rating 9)
LEDA (rating 8)	REDUCE (rating 7)

Recommended Books

Data Structures and Algorithm Analysis in C++ (3rd Edition) by Mark Allen Weiss	Algorithms in C++: Fundamentals, Data Structures, Sorting, Searching by Robert Sedgewick	The Art of Computer Programming: Fundamental Algorithms by Donald Knuth
Davenport-Schinzel sequences and their geometric applications by M. Sharir and P. Agarwal	Data Structures and Network Algorithms by R. Tarjan

Related Problems

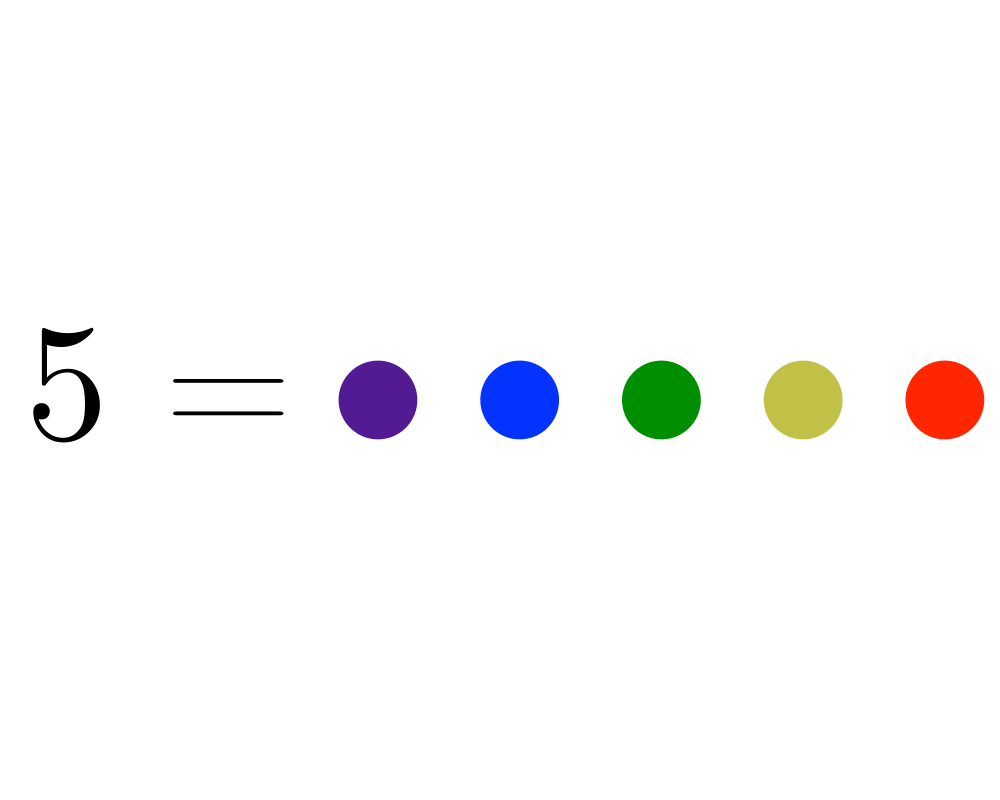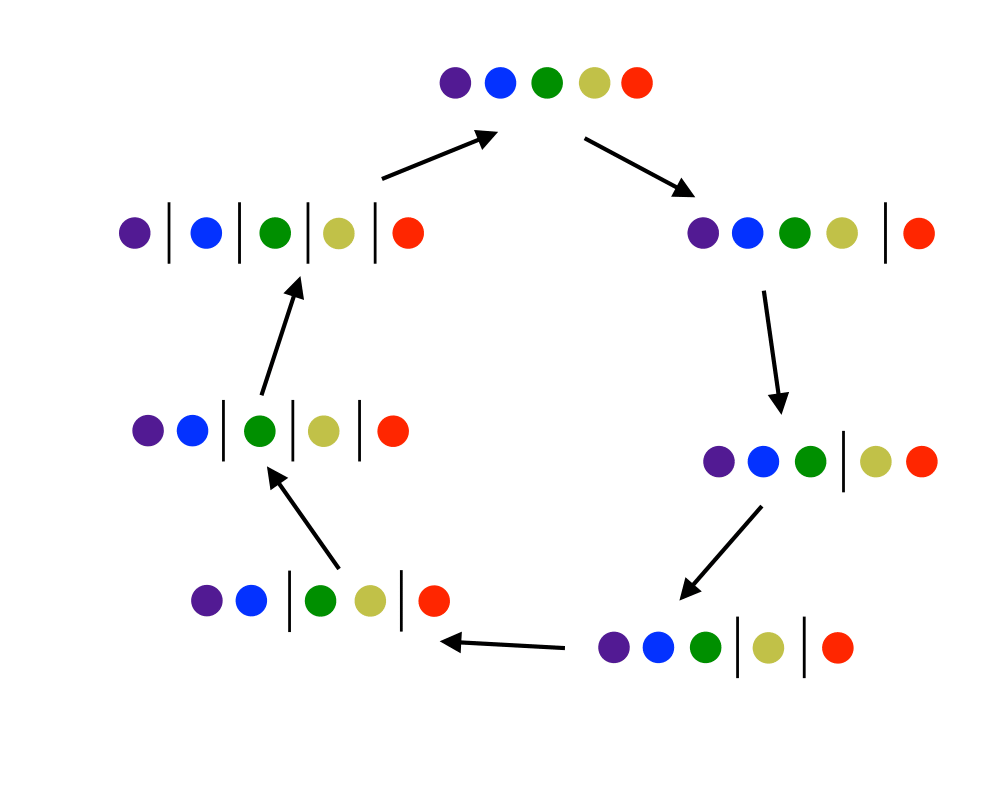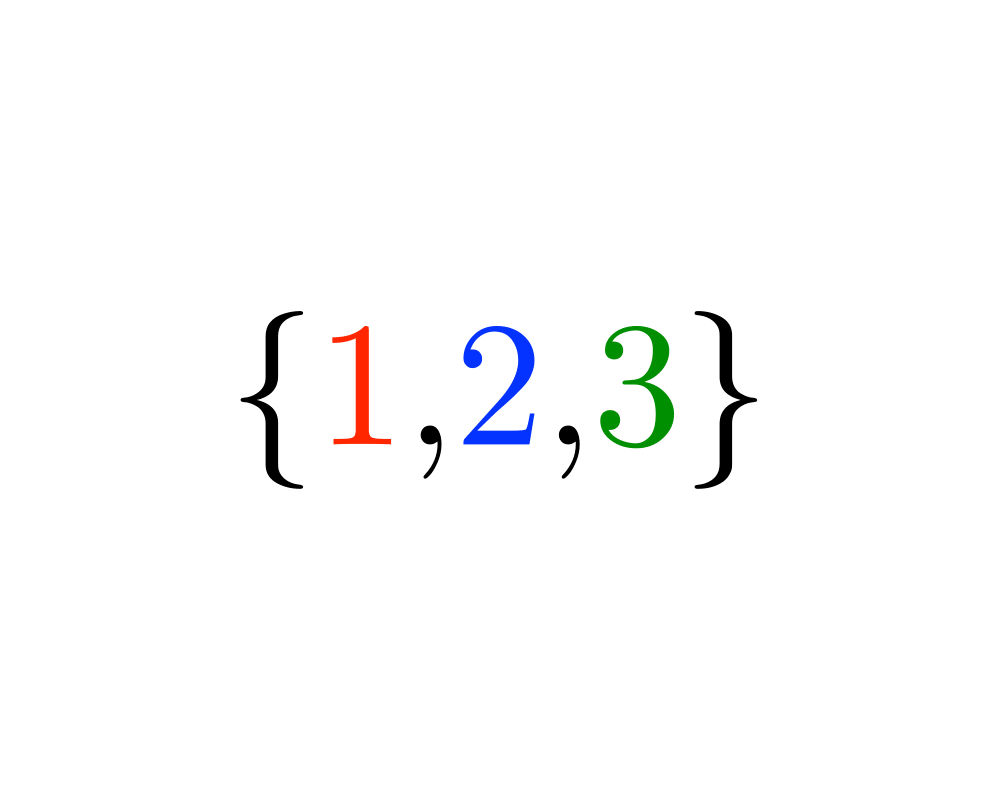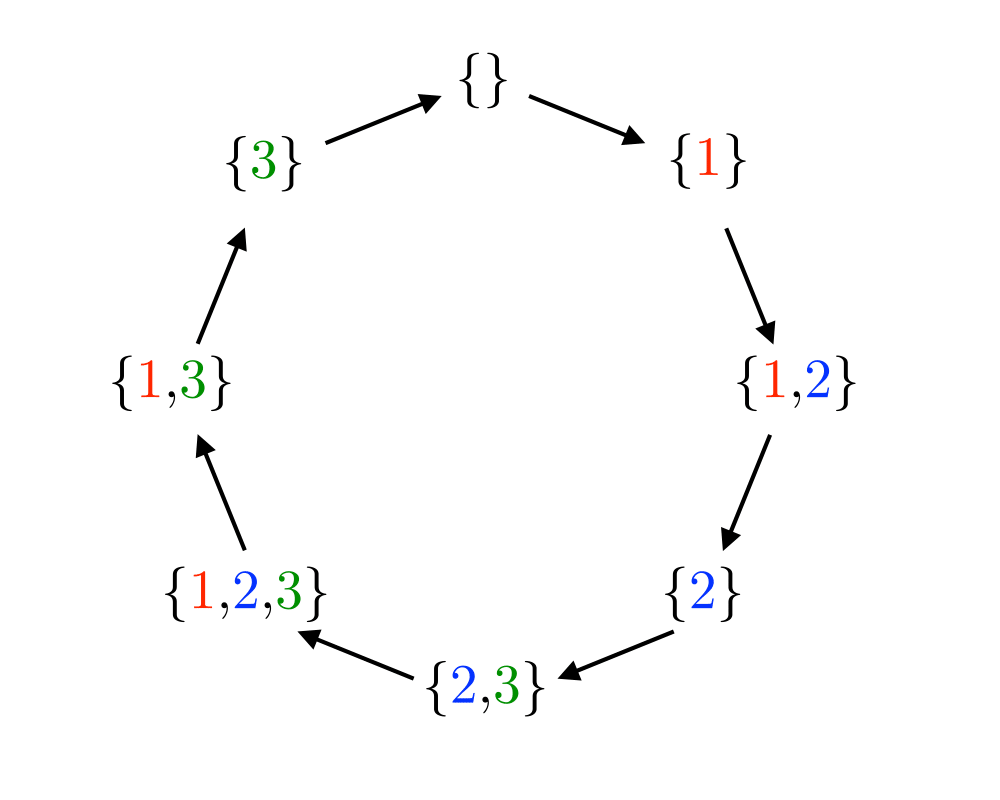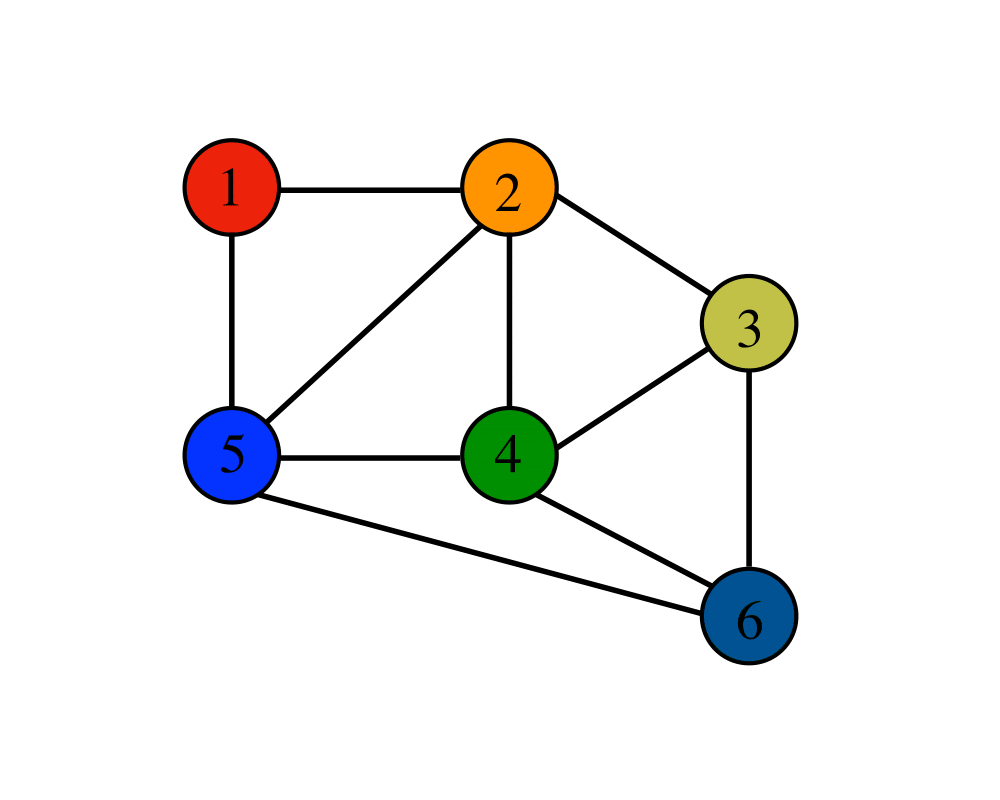Generating Partitions	Generating Subsets	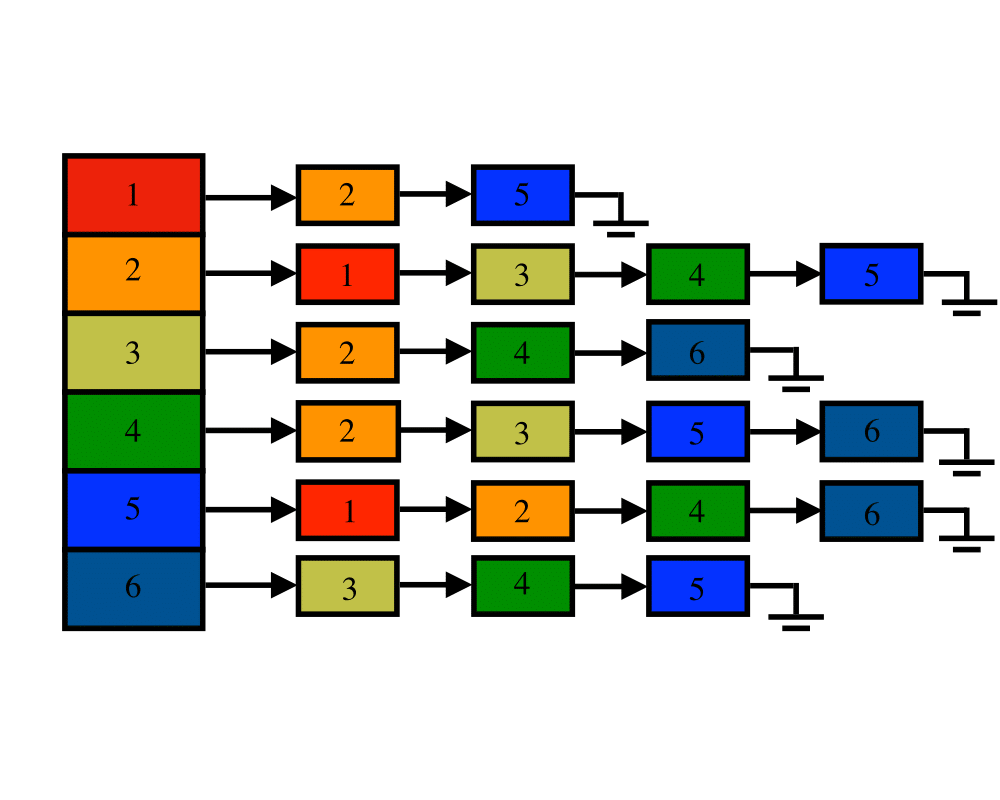Graph Data Structures
Minimum Spanning Tree	Set Cover

As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.