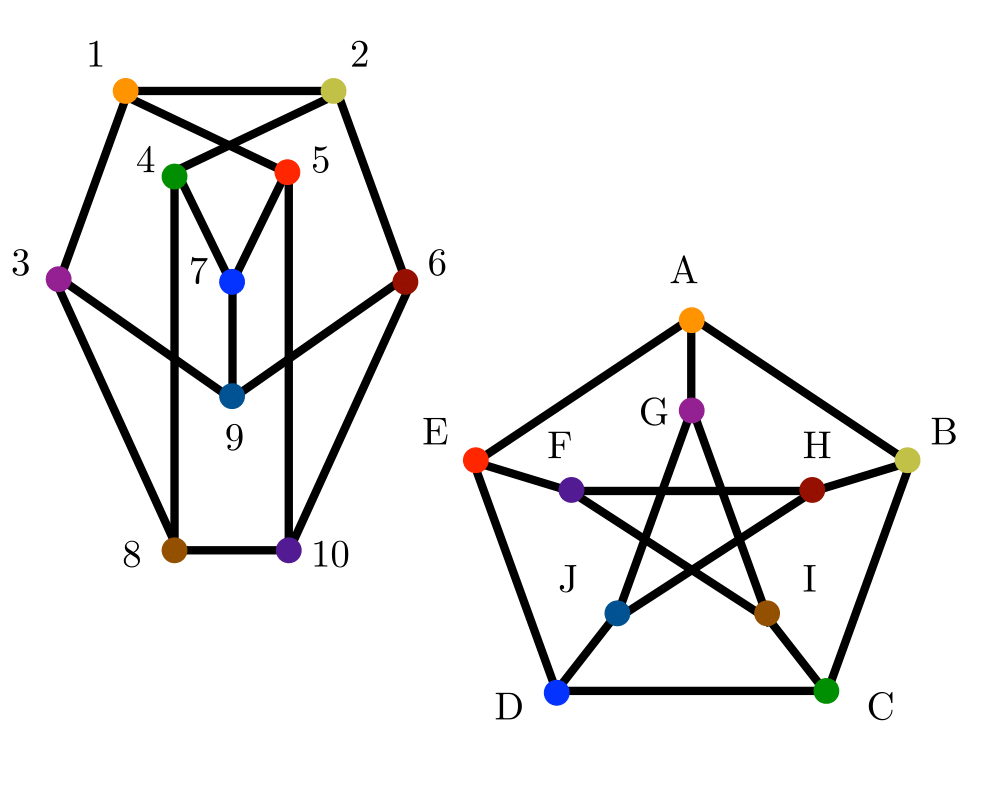
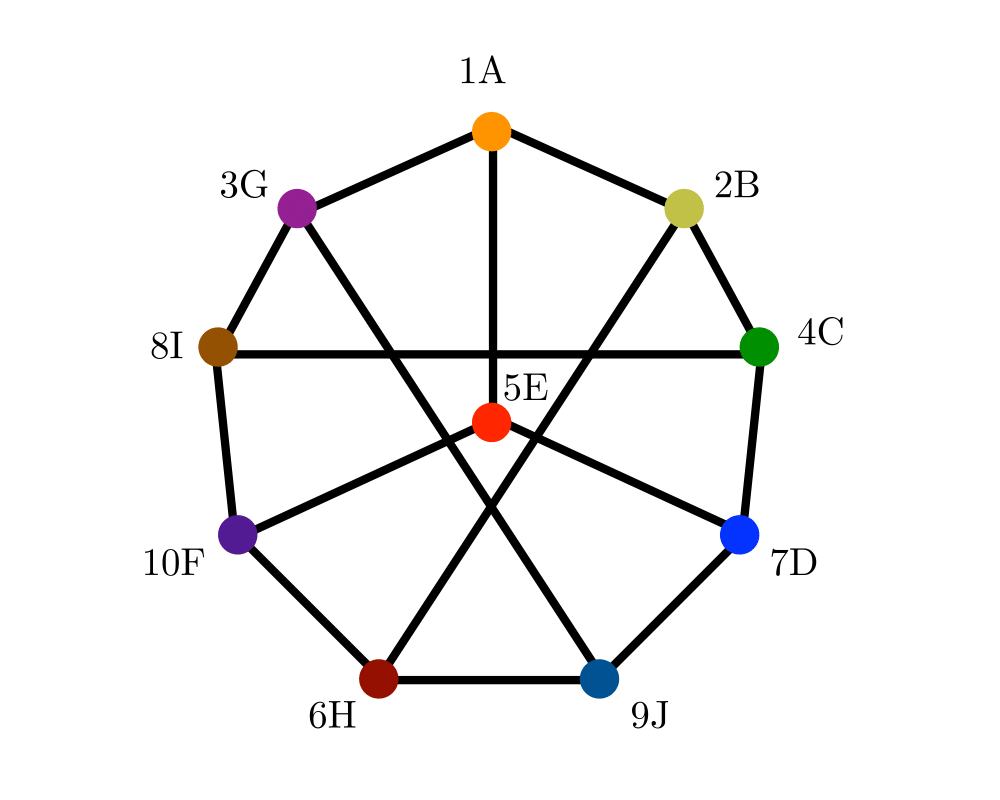
 |
 |
|
|
Input Description: Two graphs, \(g\) and \(h\).
Problem: Find a (all) mappings \(f\) of the vertices of \(g\) to the vertices of \(h\) such that \(g\) and \(h\) are identical, ie. \((x,y)\) is an edge of \(g\) iff \((f(x),f(y))\) is an edge of \(h\).
Excerpt from The Algorithm Design Manual: Isomorphism is the problem of testing whether two graphs are really the same. Suppose we are given a collection of graphs and must perform some operation on each of them. If we can identify which of the graphs are duplicates, they can be discarded so as to avoid redundant work.
We need some terminology to settle what is meant when we say two graphs are the same. Two labeled graphs \(G=(V_g,E_g)\) and \(H=(V_h,E_h)\) are identical when \((x,y) \in Eg\) iff \((x,y) \in E_h\). The isomorphism problem consists of finding a mapping from the vertices of \(G\) to \(H\) such that they are identical. Such a mapping is called an isomorphism.
Identifying symmetries is another important application of graph isomorphism. A mapping of a graph to itself is called an automorphism, and the collection of automorphisms (its automorphism group) provides a great deal of information about symmetries in the graph. For example, the complete graph \(K_n\) has \(n!\) automorphisms (any mapping will do), while an arbitrary random graph is likely to have few or perhaps only one, since \(G\) is always identical to itself.
| NAUTY (rating 10) |
VFLib (rating 9) |
| GraphBlast (rating 9) |
CAGES (rating 8) |
| HyperGraphLib (rating 6) |
fraciso (rating 5) |
| GMT (rating 5) |
Combinatorica (rating 3) |
  Generating Graphs |
  Shape Similarity |
  Shortest Path |
  String Matching |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
Mining Graph Data by D. Cook and L. Holder
The Graph Isomorphism Problem: its structural complexity by J. Kobler, U. Schöning, and J. Toran
Distances in Graphs by F. Buckley and F. Harary
Group-theoretic algorithms and graph isomorphism by C. M. Hoffmann
The Design and Analysis of Computer Algorithms by A. Aho and J. Hopcroft and J. Ullman