 |
 |
 |
 |
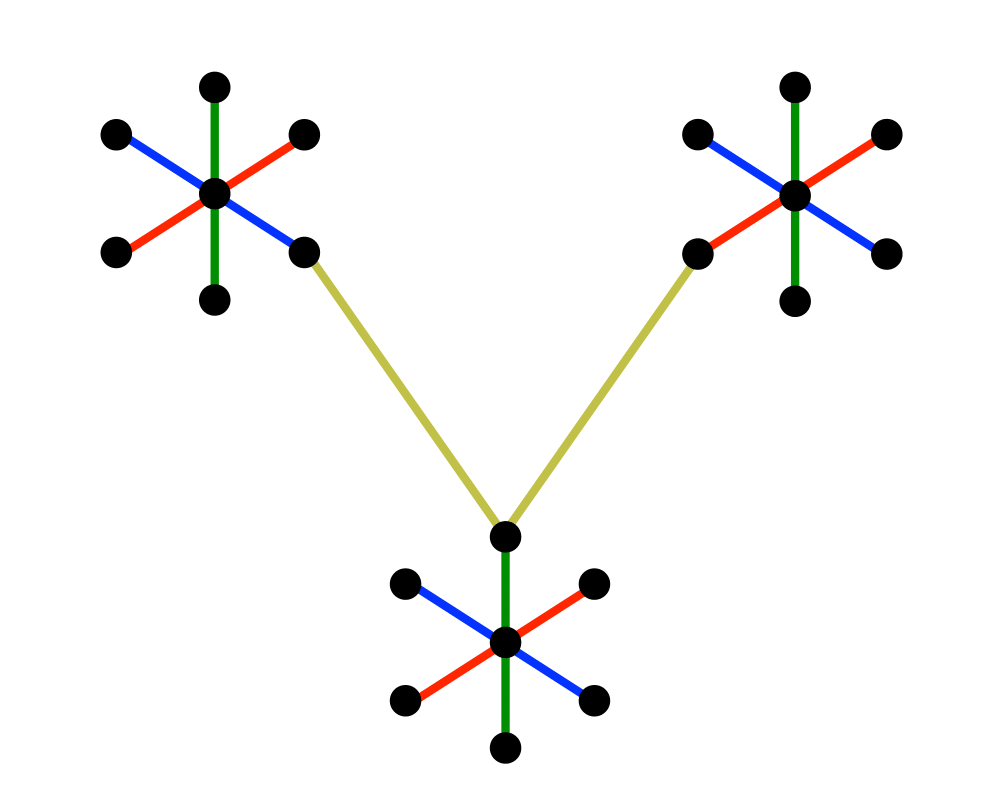
Input Description: A graph \(G = (V,E)\) with weighted edges.
Problem: The subset of \(E\) of \(G\) of minimum weight which forms a tree on \(V\).
Excerpt from The Algorithm Design Manual: The minimum spanning tree (MST) of a graph defines the cheapest subset of edges that keeps the graph in one connected component. Telephone companies are particularly interested in minimum spanning trees, because the minimum spanning tree of a set of sites defines the wiring scheme that connects the sites using as little wire as possible. It is the mother of all network design problems.
Minimum spanning trees prove important for several reasons:
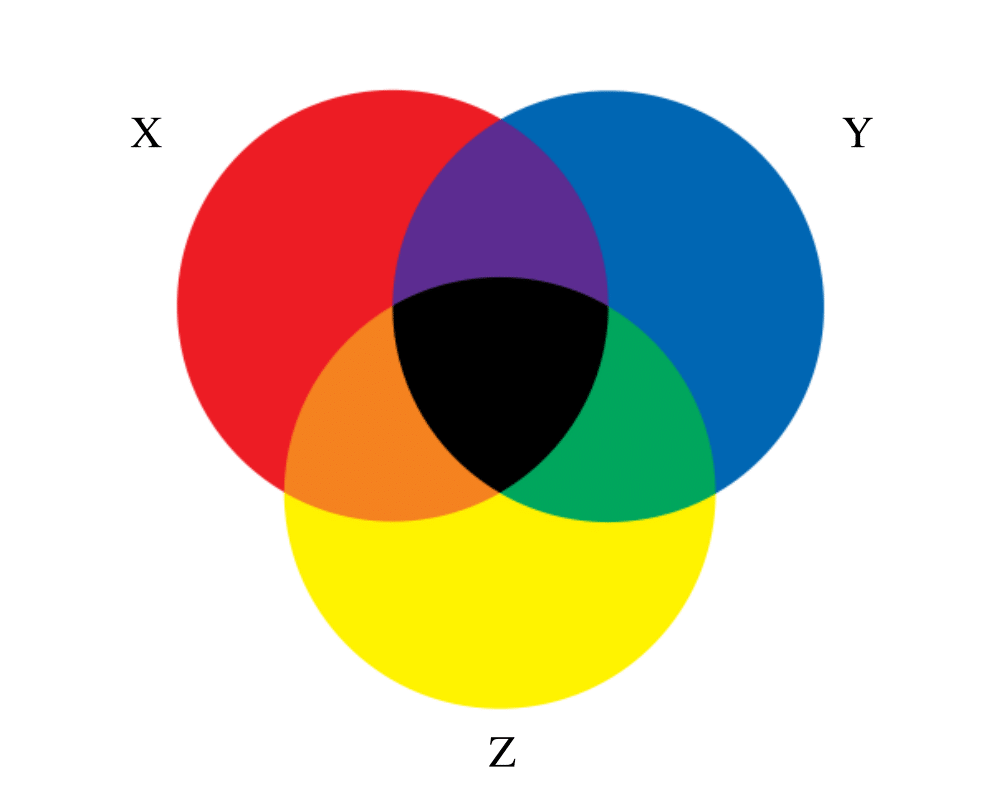  Set Data Structures |
 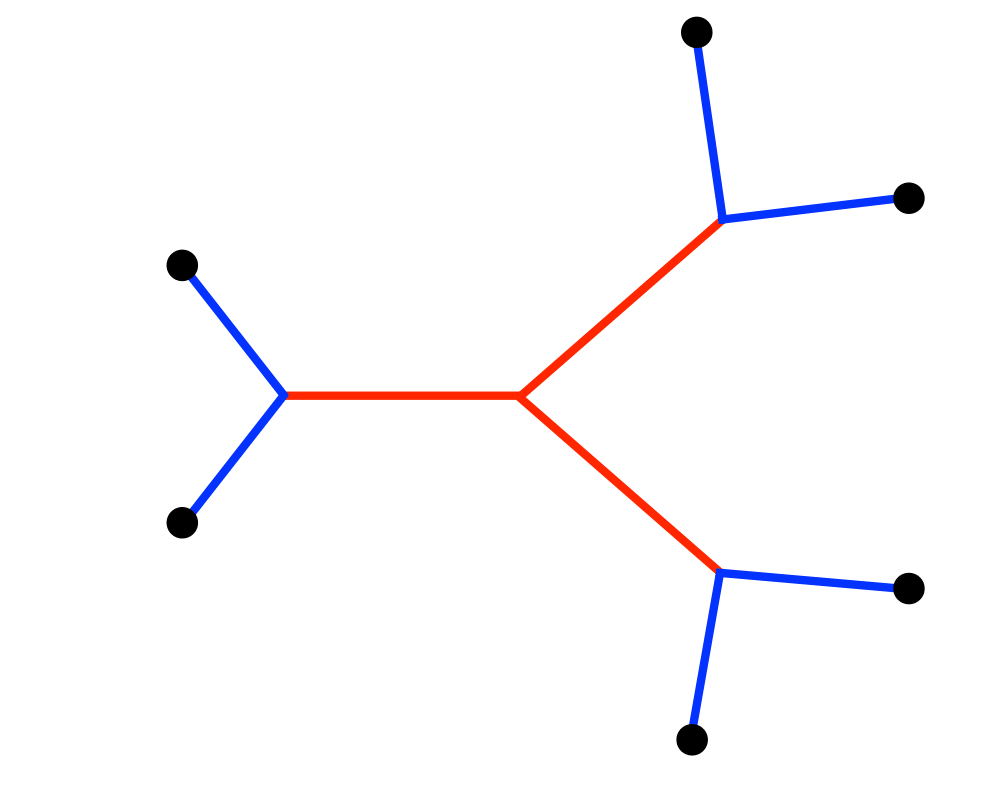 Steiner Tree |
  Traveling Salesman Problem |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.