 |
 |
|
|
Input Description: A weighted graph \(G\).
Problem: Find the cycle of minimum cost visiting all of the vertices of \(G\) exactly once.
Excerpt from The Algorithm Design Manual: The traveling salesman problem is the most notorious NP-complete problem. This is a function of its general usefulness, and because it is easy to explain to the public at large. Imagine a traveling salesman who has to visit each of a given set of cities by car.
Although the problem arises in transportation applications, its most important applications arise in optimizing the tool paths for manufacturing equipment. For example, consider a robot arm assigned to solder all the connections on a printed circuit board. The shortest tour that visits each solder point exactly once defines the most efficient path for the robot. A similar application arises in minimizing the amount of time taken by a graphics plotter to draw a given figure.
| Concorde (rating 10) |
TSP solvers (rating 9) |
| GOBLIN (rating 9) |
Keld Helsgaun's traveling salesman (rating 8) |
| GeneticAlgorithm-TSP (rating 6) |
tsp-solver (rating 6) |
| JGraphT (rating 5) |
Netlib (rating 4) |
 The Traveling Salesman Problem and Its Variations by G. Gutin and A. Punnen |
 The Traveling Salesman Problem : A Guided Tour of Combinatorial Optimization by E.L. Lawler (Editor) and A. H. Rinnooy-Kan |
  Convex Hull |
  Hamiltonian Cycle |
  Minimum Spanning Tree |
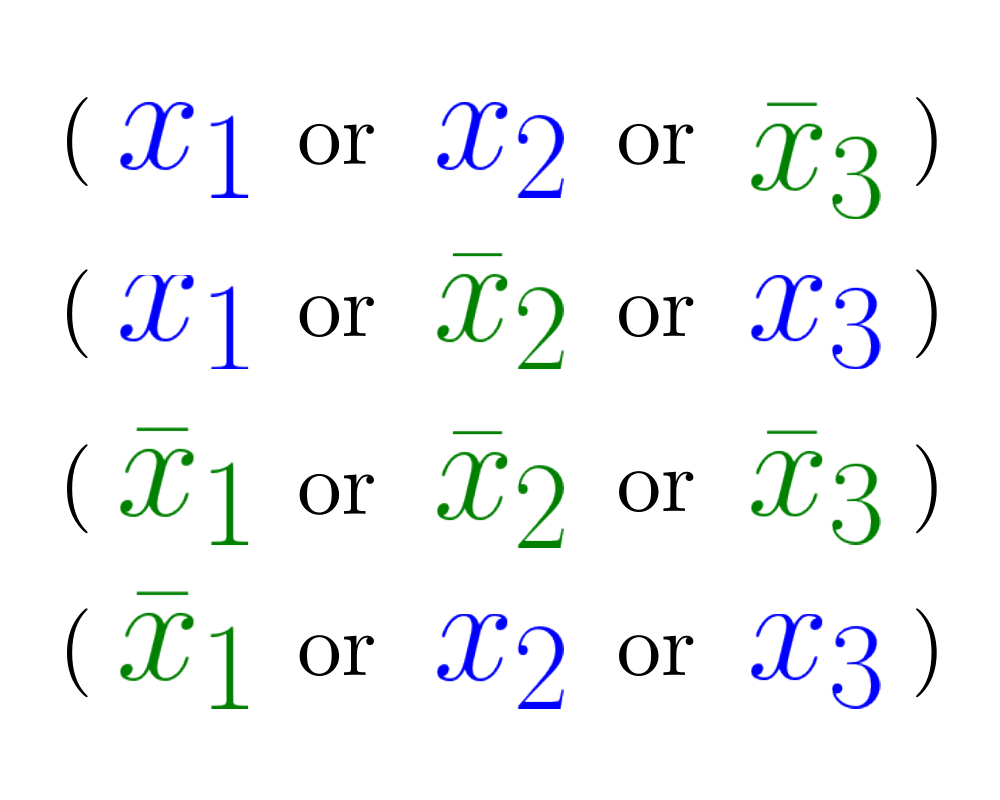  Satisfiability |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.