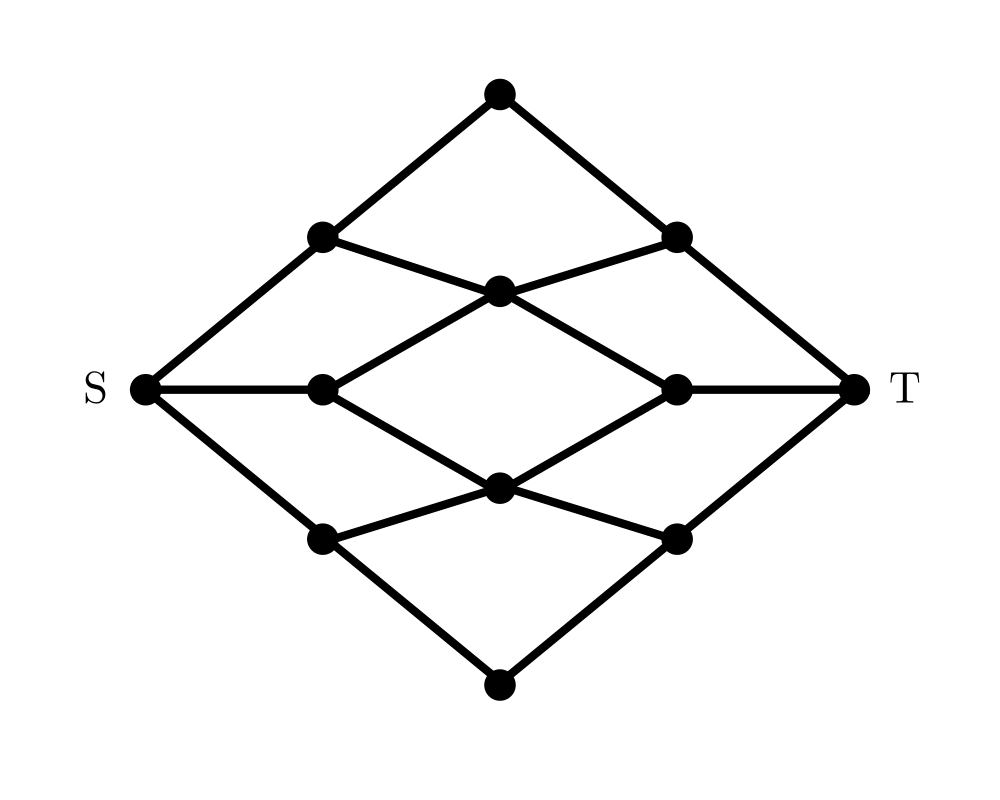
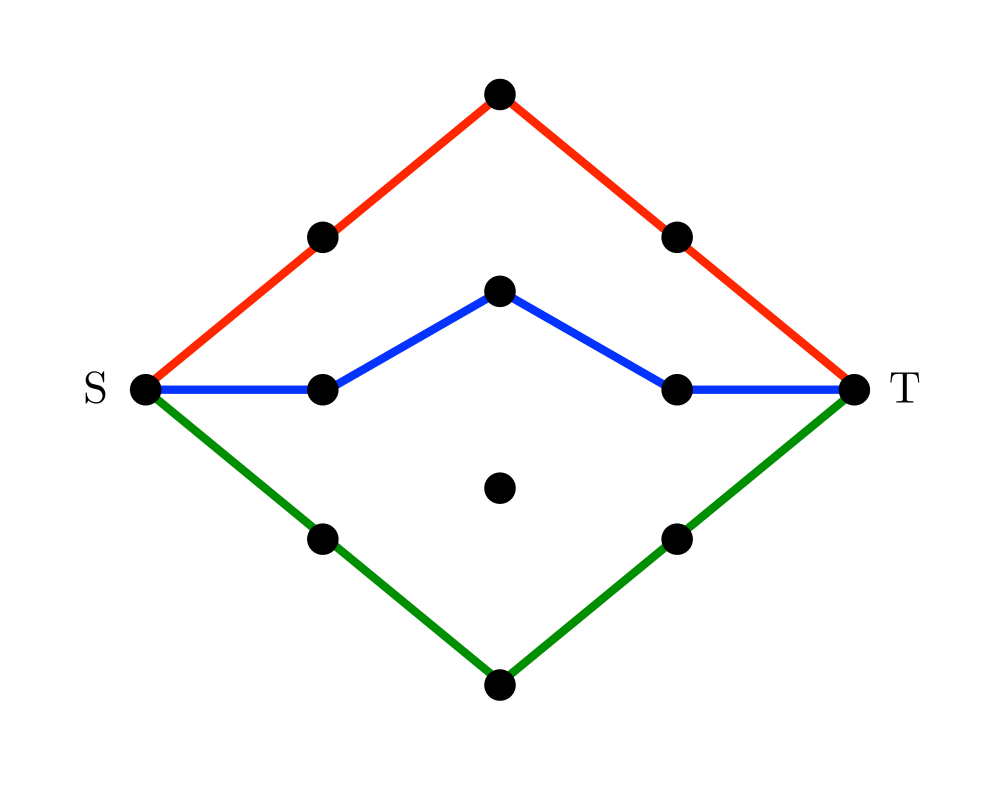
 |
 |
|
|
Input Description: A graph \(G\), where each edge \((i,j)\) has a capacity \(c_{i,j}\). A source node \(s\) and sink node \(t\).
Problem: What is the maximum flow you can route from \(s\) to \(t\) while respecting the capacity of each edge.
Excerpt from The Algorithm Design Manual: Applications of network flow go far beyond plumbing. Finding the most cost-effective way to ship goods between a set of factories and a set of stores defines a network flow problem, as do resource-allocation problems in communications networks and a variety of scheduling problems.
The real power of network flow is that a surprising variety of linear programming problems that arise in practice can be modeled as network flow problems, and that special-purpose network flow algorithms can solve such problems much faster than general-purpose linear programming methods. Several of the graph problems we have discussed in this book can be modeled as network flow, including bipartite matching, shortest path, and edge/vertex connectivity.
| GOBLIN (rating 10) |
Goldberg's Network Optimization Codes (rating 10) |
| NEOS (rating 9) |
LEDA (rating 8) |
| RAPID (rating 8) |
PyMaxflow (rating 6) |
| Graph-Theory-Ford-Fulkerson-Maximum-Flow (rating 6) |
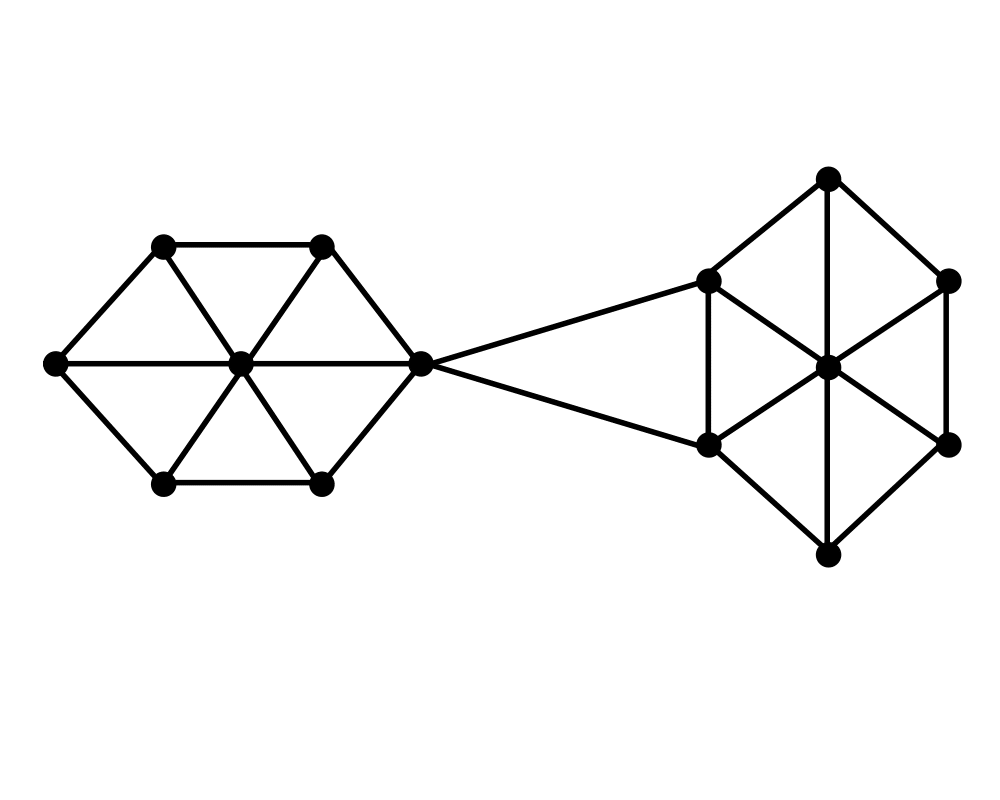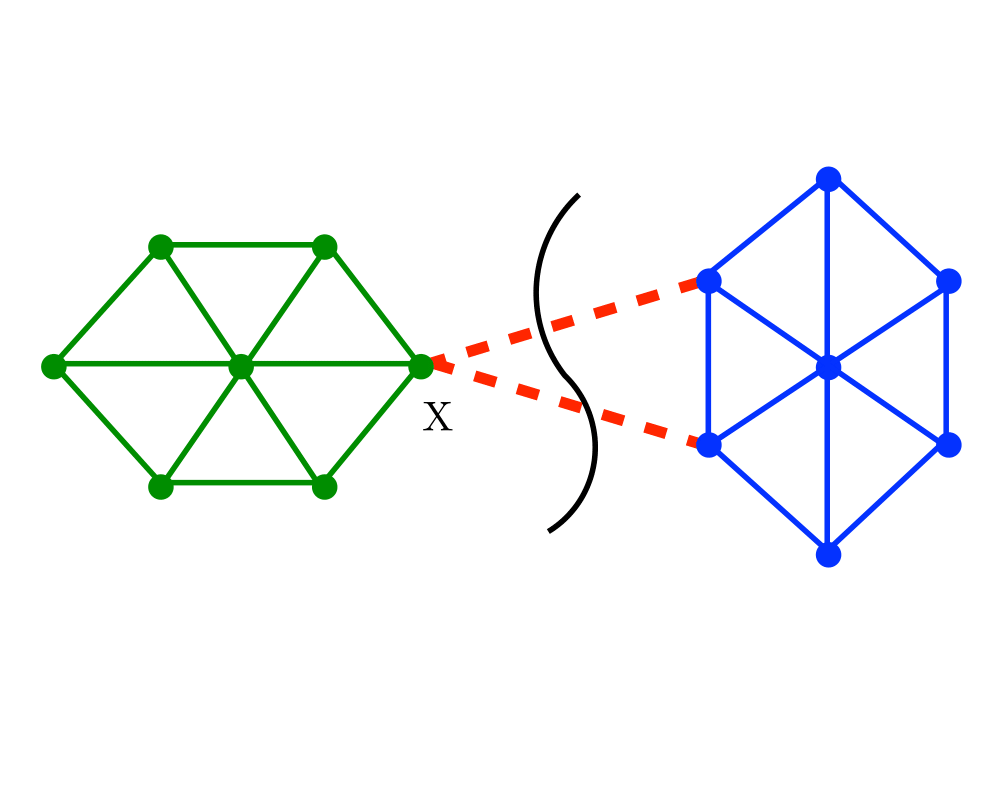  Edge and Vertex Connectivity |
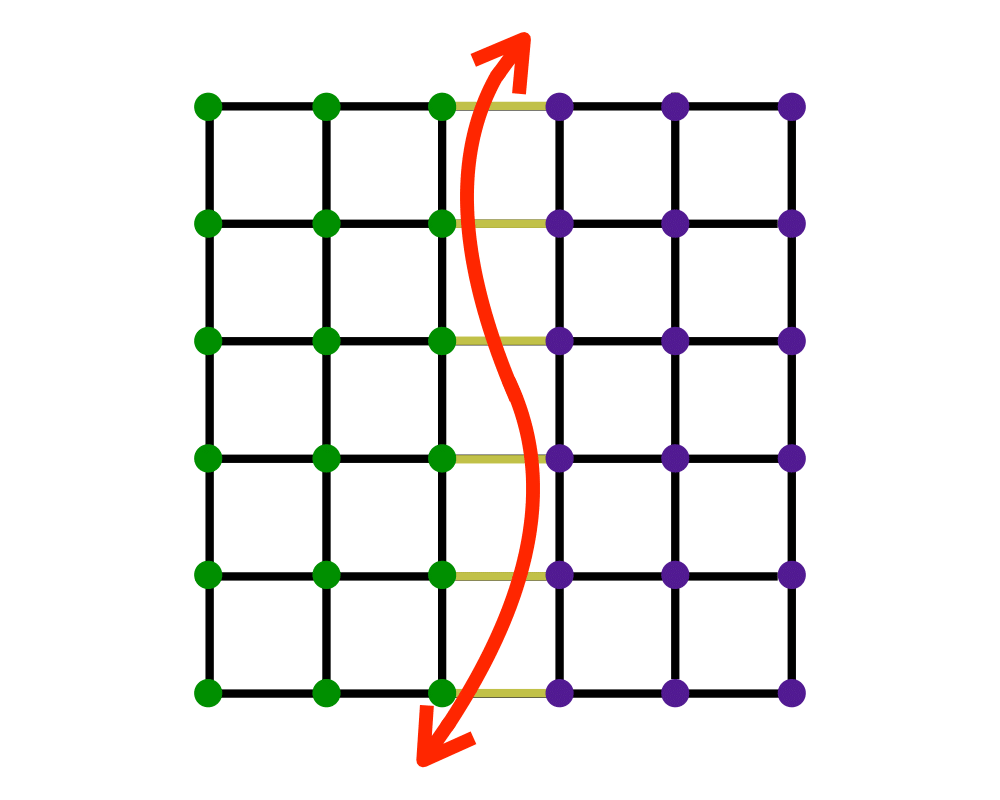  Graph Partition |
  Linear Programming |
  Matching |
  Shortest Path |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
Network Coding Theory by R Yeung and S-Y. Li and N. Cai and Z. Zhang
Network Flows : Theory, Algorithms, and Applications by Ravindra K. Ahuja, Thomas L. Magnanti, and James B. Orlin
Introduction to Algorithms by T. Cormen and C. Leiserson and R. Rivest and C. Stein
Flows in Networks by L. Ford and D. R. Fulkerson